嵌套多芒星的全着色

苏榕进; 方刚; 朱恩强; 许进

doi:10.11999/JEIT250861

嵌套多芒星的全着色

doi: 10.11999/JEIT250861 cstr: 32379.14.JEIT250861

苏榕进^{1, 2},
方刚¹,
朱恩强^1, ,,
许进³

1.
广州大学计算科技研究院广州 510555
2.
广州大学计算机科学与网络工程学院广州 510555
3.
北京大学高可信软件技术教育部重点实验室；北京大学计算机学院北京 100871

基金项目: 国家自然科学基金(62272115, 62541308)

详细信息

作者简介:
苏榕进：男，硕士生，研究方向为图论及其应用

方刚：男，教授，研究方向为生物计算、模式识别

朱恩强：男，教授，研究方向为图论及其应用、组合优化

许进：男，教授，研究方向为理论计算机、图论与组合优化

通讯作者:
朱恩强　sailingzeq@gmail.com

中图分类号: O157.5
计量
- 文章访问数: 61
- HTML全文浏览量: 24
- PDF下载量: 5
- 被引次数: 0
出版历程
- 修回日期: 2026-01-12
- 录用日期: 2026-01-12
- 网络出版日期: 2026-01-24

Total Coloring on Planar Graphs of Nested n-Pointed Stars

SU Rongjin^{1, 2},
FANG Gang¹,
ZHU Enqiang^{1
, ,},
XU Jin³

1.
Institute of Computing Science and Technology, Guangzhou University, Guangzhou 510555, China
2.
School of Computer Science and Cyber Engineering, Guangzhou University, Guangzhou 510555, China
3.
School of Computer Science, Peking University, Beijing 100871, China

Funds: The National Natural Science Foundation of China (62272115, 62541308)

摘要

摘要: 图G的k-全着色是指使用k种颜色对图的顶点与边同时进行着色，使得任意相邻的顶点、相邻的边，以及任意关联的顶点与边之间均着不同颜色。全着色猜想断言：任何简单图均存在(Δ+2)-全着色，其中Δ代表图的最大度。自该猜想提出以来，一直受到广泛关注，并取得了丰富的研究进展。然而，尽管经过数十年的努力，全着色猜想至今仍未得到完全证明，甚至对平面图情形亦不例外。目前，对于平面图，仅剩最大度为6且同时含有4-扇子结构，或最大平均度不低于23/5的图类尚未被证实。本文针对这类平面图的全着色展开研究，提出了一类称为嵌套多芒星的图类，其最大度为6、包含4-扇子结构，且最大平均度不低于23/5。我们证明了全着色猜想在此类图上成立。特别地，我们发现一类属于I-型图的嵌套多芒星，即存在7-全着色。这一结果进一步推进了对平面图全着色问题的理解。
- 全着色 /
- 平面图 /
- 嵌套多芒星 /
- I-型图
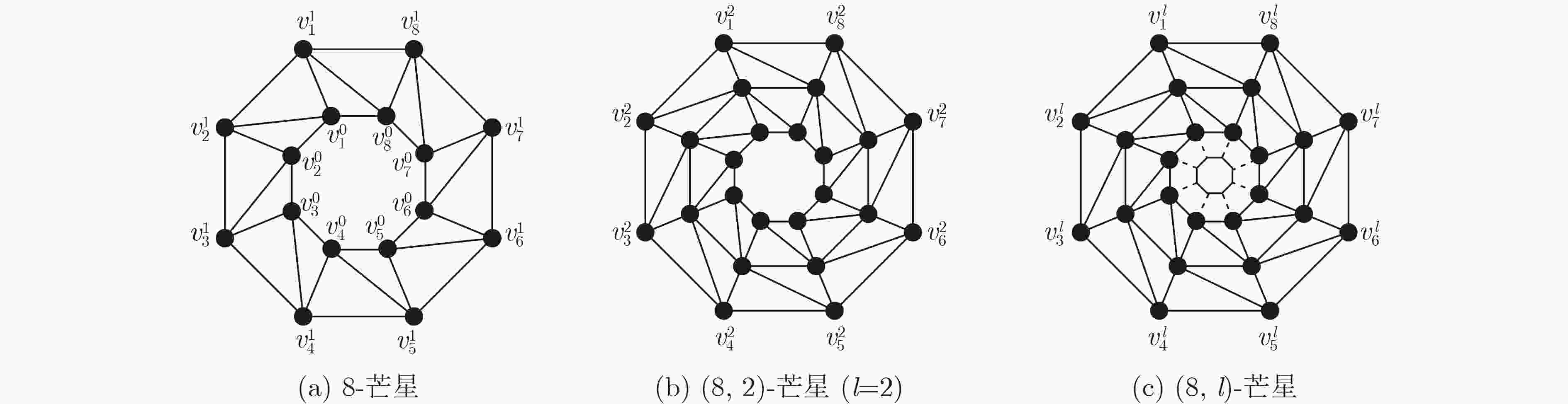
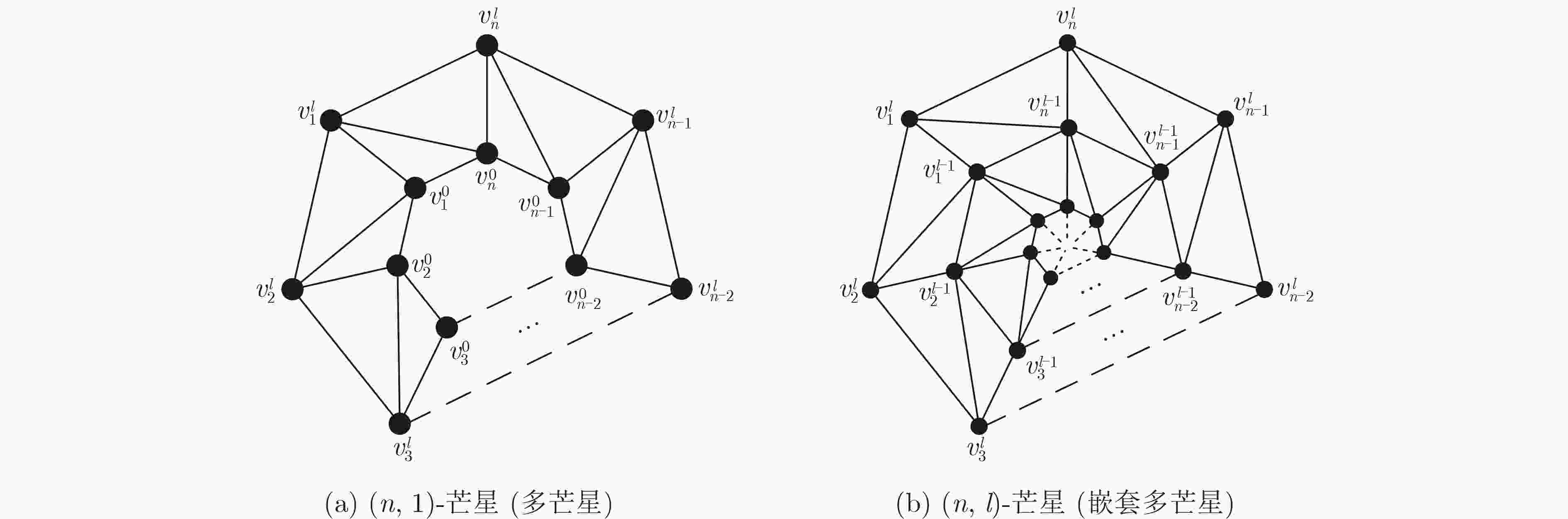
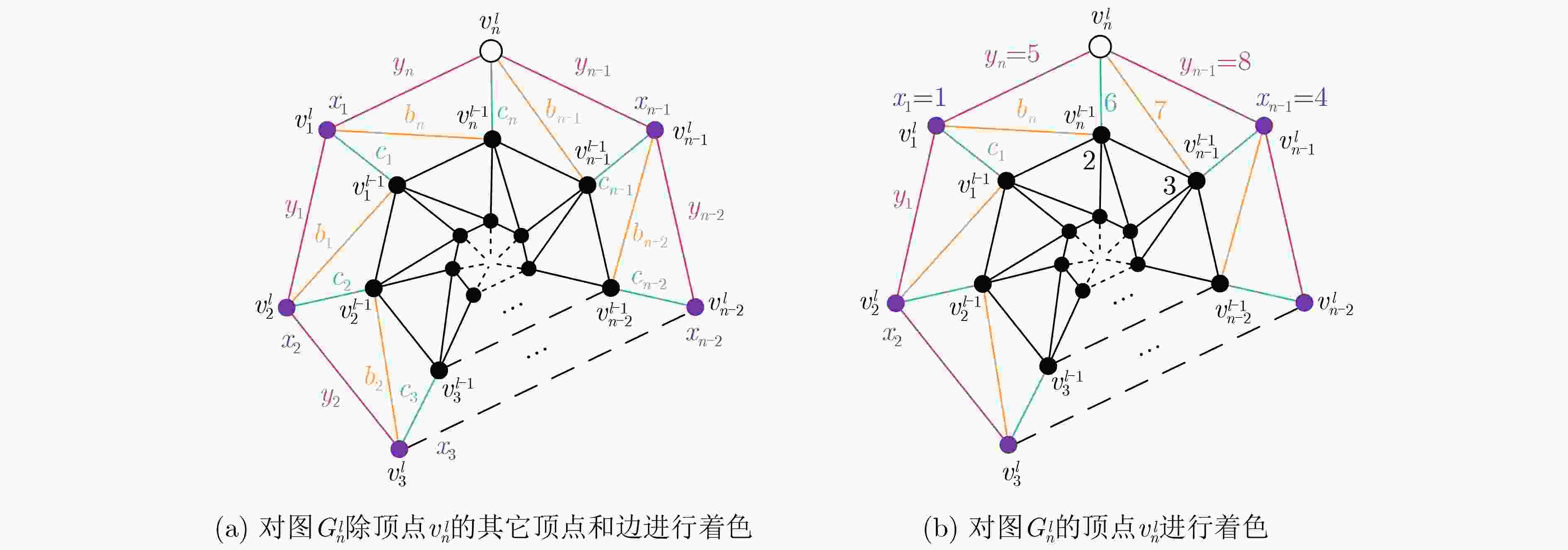
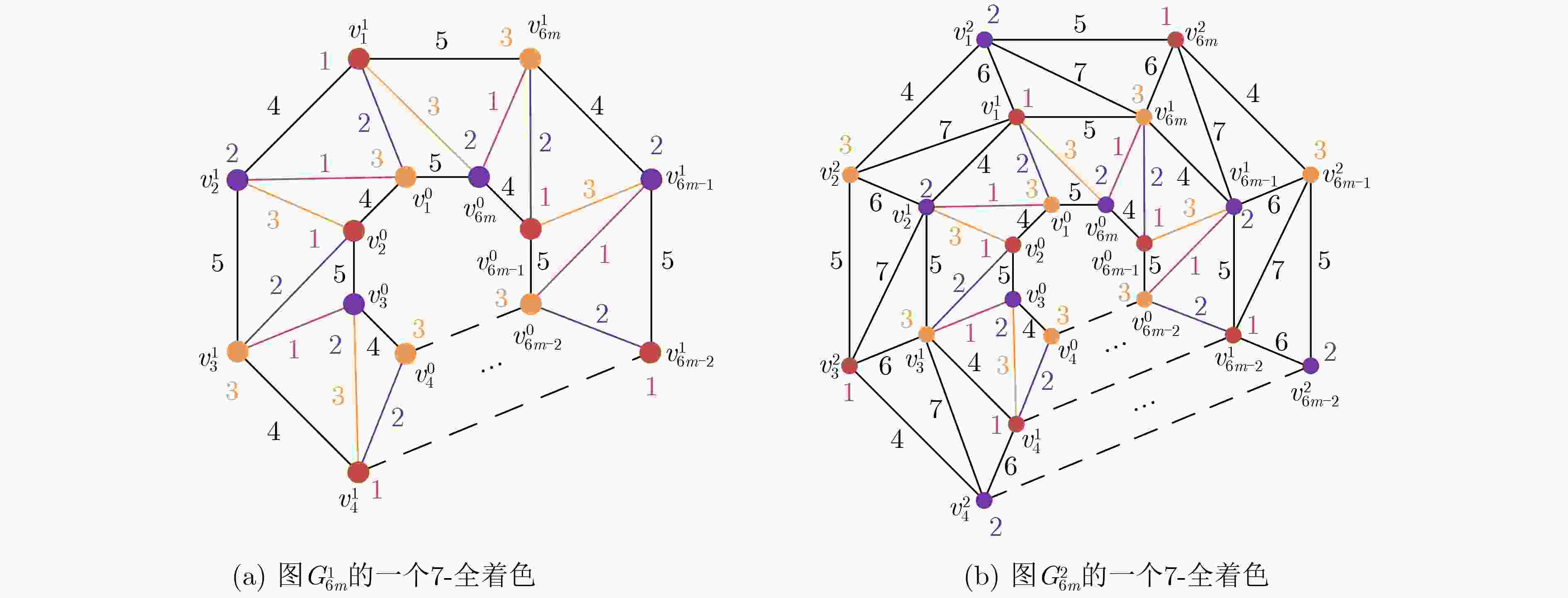
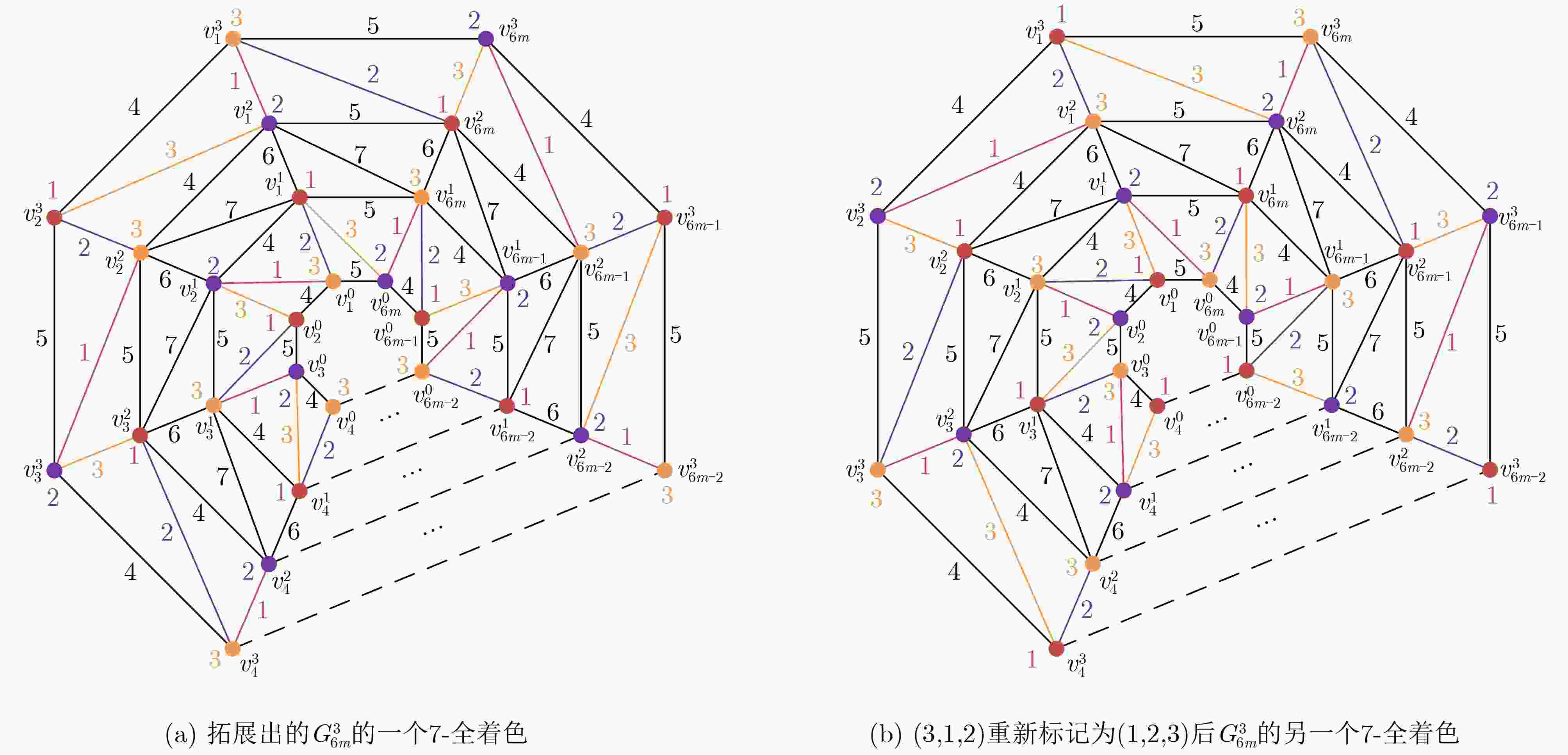
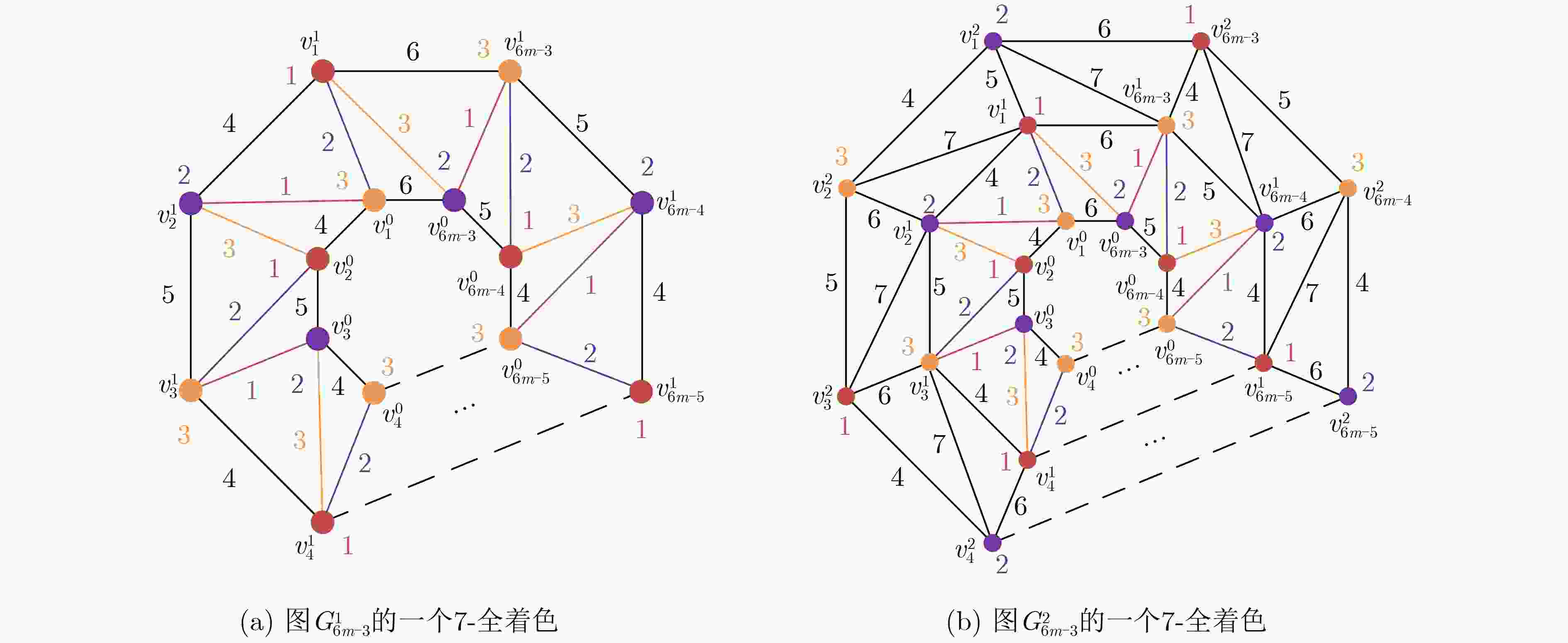
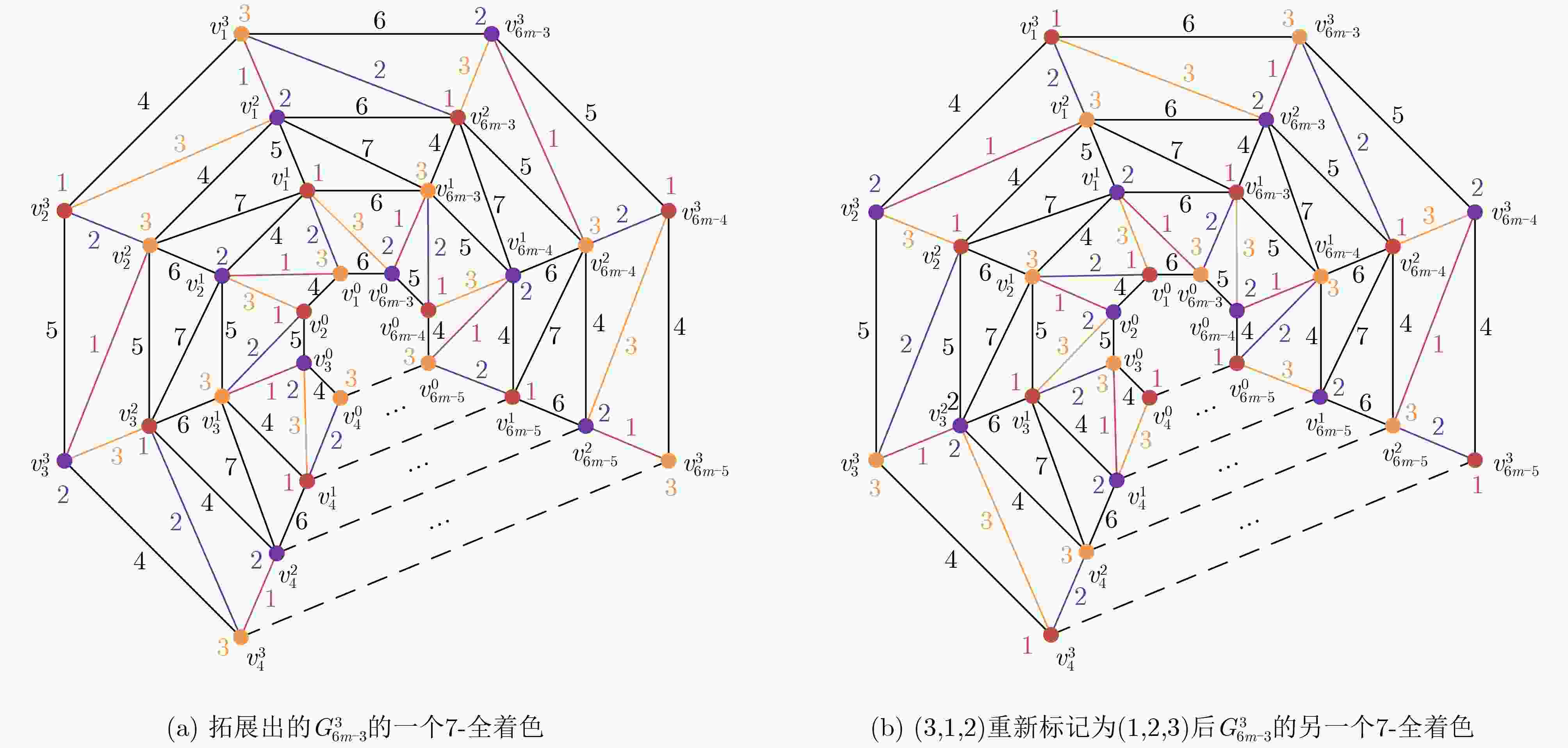
Abstract: Objective Various kinds of combinatorial optimization problems in real life can be regarded as graph coloring problems. One classic theme in graph coloring is total coloring that combines vertex coloring and edge coloring. Both previous results and present researches about total coloring center on the famous Total Coloring Conjecture (TCC), which was proposed in the 1960s. Researchers have been trying to find solutions. For those graphs (including planar graphs) with low maximum degree, specifically of less than six, the correctness of TCC has been verified through enumerating the maximum degree. A powerful and wonderful discharging technique is utilized to prove that TCC holds for planar graphs with high maximum degree, specifically of more than six. This method is conducive to solve many problems regarding planar graphs involves identifying some reducible configurations and formulating detailed discharging rules. However, when the discharging method is employed to cope with the case where planar graphs have maximum degree of exactly six, it becomes limited. In this complex case, researchers have found certain graphs that satisfying TCC. These graphs are subject to certain constraints, such as the graphs free of cycles of length four and the graphs without two adjacent triangles. Additionally, it is improved in recent results. It is demonstrated that TCC holds for those planar graphs free of 4-fan subgraphs and for those planar graphs with maximum average degree of less than twenty-three fifths. Hence, one still may not confirm that whether planar graphs with maximum degree of six which contain a 4-fan subgraph or have maximum average degree of not less than twenty-three fifths satisfy the TCC. In order to verify that whether TCC is applicable for such graphs, this paper explores total coloring on one kind of such planar graphs, called nested n-pointed stars. It is aimed to show that TCC holds for nested n-pointed stars. Methods This article mainly adopts methods regarding theoretical research. One of these methods is the well-established mathematical induction which is widely used to prove theorems, especially those containing countable parameters. Another one is construction method, demanding constructing instances to support propositions. Method of listing cases is also exploited for completeness and clarity of statements. To start with, an n-pointed star is obtained, through connecting each outer side of an n-polygon (n≥3) to each triangle and then connecting all the vertices of these triangles not appearing on this n-polygon one by one into a new n-polygon. Based on the new n-polygon, a nested n-pointed star with l layers, denoted by $ G_{n}^{l} $, is formed by iterating the operation layer by layer. The nested n-pointed stars obtained in this way have maximum degree of exactly six. The properties that nested n-pointed stars contain 4-fan subgraphs and have maximum average degree of large than twenty-three fifths are determined. As nested n-pointed stars are iterative planar graphs, mathematical induction is used by induction on the number of layers of $ G_{n}^{l} $ to demonstrate that nested n-pointed stars have a total 8-coloring by following steps: (1) Show that $ G_{n}^{1} $ has a total 8-coloring; (2) Suppose that $ G_{n}^{l-1} $ has a total 8-coloring; (3) Prove that $ G_{n}^{l} $ has a total 8-coloring. Further, a nested n-pointed star $ G_{n}^{l} $ will be referred as type I graph if it admits a total 7-coloring. When $ n=3k $, construction method is utilized to present that $ G_{3k}^{l} $ is type I graph. The value of $ k $ is classified as odd number $ (k=2m-1) $ and even number $ (k=2m) $. In each case, a total 7-coloring of $ G_{3k}^{l} $ is obtained by assigning colors to all the vertices and edges directly. Results and Discussions It is demonstrated by induction on the number of layers of $ G_{n}^{l} $ that nested n-pointed stars follow the Total Coloring Conjecture (as illustrated in Fig. 5). Only five distinct colors are assigned to vertices and edges of $ G_{3k}^{1} $ to identify a special total 5-coloring of $ G_{3k}^{1} $(see Fig. 6(a) and Fig. 8(a)). The other two colors are alternately assigned to the edges connecting two polygons lying on layer 1 and layer 2. Then a total 7-coloring of $ G_{3k}^{2} $ is gotten by coloring the vertices and edges of the polygon lying on layer 2 (see Fig. 6(b) and Fig. 8(b)). Next, it is extended to a total 7-coloring of $ G_{3k}^{3} $ (see Fig. 7(a) and Fig. 9(a)). After performing a permutation operation, another total 7-coloring of $ G_{3k}^{3} $ is obtained (see Fig. 7(b) and Fig. 9(b)). The coloring pattern on the outermost layer of this total 7-coloring is exactly the same as that on the outermost layer of $ G_{3k}^{1} $, which means that a total 7-coloring of $ G_{3k}^{4},G_{3k}^{5},\cdots ,G_{3k}^{l} $ can be obtained in the same extension way. Therefore, $ G_{3k}^{l} $ is type I graph. Conclusions This paper verifies that Total Coloring Conjecture holds for nested n-pointed stars, which have maximum degree of exactly 6 and contain 4-fan subgraphs. It shows that $ G_{3k}^{l} $ is type I graph. Then, a question arises: whether $ G_{n}^{l} $ is type I graph when $ n\neq 3k $. It is not hard to construct a total 7-coloring of $ G_{n}^{l} $ if $ n=4 $ or $ n=5 $, and therefore both $ G_{4}^{l} $ and $ G_{5}^{l} $ are type I graphs. For other $ n\neq 3k $, whether $ G_{n}^{l} $ is type I graph remains to be determined.
- Total coloring /
- Planar graphs /
- Nested n-pointed stars /
- Type I graphs

HTML全文

图 1 一个7-全着色实例

下载: 全尺寸图片幻灯片

图 2 一个4-扇

下载: 全尺寸图片幻灯片

图 3 嵌套8-芒星

下载: 全尺寸图片幻灯片

图 4 多芒星和嵌套多芒星

下载: 全尺寸图片幻灯片

图 5 对图$ G_{n}^{l} $的顶点和边进行全着色

下载: 全尺寸图片幻灯片

图 6 $ G_{6m}^{1} $的7-全着色和$ G_{6m}^{2} $的7-全着色

下载: 全尺寸图片幻灯片

图 7 $ G_{6m}^{3} $的两个7-全着色

下载: 全尺寸图片幻灯片

图 8 $ G_{6m-3}^{1} $的7-全着色和$ G_{6m-3}^{2} $的7-全着色

下载: 全尺寸图片幻灯片

图 9 $ G_{6m-3}^{3} $的两个7-全着色

下载: 全尺寸图片幻灯片

参考文献(26)

[1]	BEHZAD M. Graphs and their chromatic numbers[D]. [Ph. D. dissertation], Michigan State University, 1965.
[2]	VIZING V G. Some unsolved problems in graph theory[J]. Russian Mathematical Surveys, 1968, 23(6): 125–141. doi: 10.1070/RM1968v023n06ABEH001252.
[3]	ROSENFELD M. On the total coloring of certain graphs[J]. Israel Journal of Mathematics, 1971, 9(3): 396–402. doi: 10.1007/BF02771690.
[4]	VIJAYADITYA N. On total chromatic number of a graph[J]. Journal of the London Mathematical Society, 1971, s2-3(3): 405–408. doi: 10.1112/jlms/s2-3.3.405.
[5]	KOSTOCHKA A V. The total coloring of a multigraph with maximal degree 4[J]. Discrete Mathematics, 1977, 17(2): 161–163. doi: 10.1016/0012-365X(77)90146-7.
[6]	KOSTOCHKA A V. The total chromatic number of any multigraph with maximum degree five is at most seven[J]. Discrete Mathematics, 1996, 162(1/3): 199–214. doi: 10.1016/0012-365X(95)00286-6.
[7]	DALAL A, MCDONALD J, and SHAN S L. Total coloring graphs with large maximum degree[J]. Journal of Graph Theory, 2025, 110(3): 249–262. doi: 10.1002/jgt.23268.
[8]	COUTO F, FERRAZ D A, and KLEIN S. New results on edge-coloring and total-coloring of split graphs[J]. Discrete Applied Mathematics, 2025, 360: 297–306. doi: 10.1016/j.dam.2024.09.008.
[9]	DALAL A and PANDA B S. On total chromatic number of complete multipartite graphs[J]. Discrete Applied Mathematics, 2025, 377: 445–458. doi: 10.1016/j.dam.2025.08.027.
[10]	PUNITHA A and JAYARAMAN G. On total coloring of triple star and lobster graphs[J]. Communications on Applied Nonlinear Analysis, 2024, 31(8s): 494–504. doi: 10.52783/cana.v31.1543.
[11]	KAVASKAR T and SUKUMARAN S. Total coloring of some graph operations[C]. Proceedings of the 10th International Conference on Algorithms and Discrete Applied Mathematics, Bhilai, India, 2024: 302–312. doi: 10.1007/978-3-031-52213-0_21.
[12]	PUNITHA A and JAYARAMAN G. Total coloring of middle graph of certain snake graph families[J]. Journal of Applied Mathematics & Informatics, 2024, 42(2): 353–366. doi: 10.14317/jami.2024.353.
[13]	KAVASKAR T and SUKUMARAN S. Total coloring of the generalized corona product of graphs[J]. Studia Scientiarum Mathematicarum Hungarica, 2025, 62(1): 1. doi: 10.1556/012.2025.04326.
[14]	BORODIN O V. On the total coloring of planar graphs[J]. Journal für die reine und angewandte Mathematik, 1989, 1989(394): 180–185. doi: 10.1515/crll.1989.394.180.
[15]	KOWALIK Ł, SERENI J S, and ŠKREKOVSKI R. Total-coloring of plane graphs with maximum degree nine[J]. SIAM Journal on Discrete Mathematics, 2008, 22(4): 1462–1479. doi: 10.1137/070688389.
[16]	YAP H P. Total Colourings of Graphs[M]. Berlin, Heidelberg: Springer, 2006: 96–103. doi: 10.1007/BFb0092895.
[17]	XU Renyu and WU Jianliang. Total coloring of planar graphs with 7-cycles containing at most two chords[J]. Theoretical Computer Science, 2014, 520: 124–129. doi: 10.1016/j.tcs.2013.08.019.
[18]	SANDERS D P and ZHAO Yue. On total 9-coloring planar graphs of maximum degree seven[J]. Journal of Graph Theory, 1999, 31(1): 67–73. doi: 10.1002/(SICI)1097-0118(199905)31:1<67::AID-JGT6>3.0.CO;2-C.
[19]	CAI Hua. Total coloring of planar graphs without chordal 7-cycles[J]. Acta Mathematica Sinica, English Series, 2015, 31(12): 1951–1962. doi: 10.1007/s10114-015-4337-y.
[20]	WANG Yingqian, SHANGGUAN M L, and LI Qiao. On total chromatic number of planar graphs without 4-cycles[J]. Science in China Series A: Mathematics, 2007, 50(1): 81–86. doi: 10.1007/s11434-007-2031-x.
[21]	SHEN Lan and WANG Yingqian. On the 7 total colorability of planar graphs with maximum degree 6 and without 4-cycles[J]. Graphs and Combinatorics, 2009, 25(3): 401–407. doi: 10.1007/s00373-009-0843-y.
[22]	SUN Xiangyong, WU Jianliang, WU Yuwen, et al. Total colorings of planar graphs without adjacent triangles[J]. Discrete Mathematics, 2009, 309(1): 202–206. doi: 10.1016/j.disc.2007.12.071.
[23]	ZHU Enqiang and XU Jin. A sufficient condition for planar graphs with maximum degree 6 to be totally 8-colorable[J]. Discrete Applied Mathematics, 2017, 223: 148–153. doi: 10.1016/j.dam.2017.01.036.
[24]	CHANG Yulin, JING Fei, WANG Guanghui, et al. Total-coloring of sparse graphs with maximum degree 6[J]. Acta Mathematicae Applicatae Sinica, English Series, 2021, 37(4): 738–746. doi: 10.1007/s10255-021-1039-3.
[25]	ZHU Enqiang and RAO Yongsheng. A sufficient condition for planar graphs of maximum degree 6 to be totally 7-colorable[J]. Discrete Dynamics in Nature and Society, 2020, 2020(1): 3196540. doi: 10.1155/2020/3196540.
[26]	GEETHA J, NARAYANAN N, and SOMASUNDARAM K. Total colorings-a survey[J]. AKCE International Journal of Graphs and Combinatorics, 2023, 20(3): 339–351. doi: 10.1080/09728600.2023.2187960.