基于强化学习指导模型预测控制算法的高速列车受电弓主动控制策略研究

彭宇祥; 韩志伟; 王惠; 洪玮佳; 刘志刚

doi:10.11999/JEIT250343

基于强化学习指导模型预测控制算法的高速列车受电弓主动控制策略研究

doi: 10.11999/JEIT250343 cstr: 32379.14.JEIT250343

西南交通大学电气工程学院成都 611756

详细信息

作者简介:
彭宇祥：男，硕士生，研究方向为强化学习、主动控制

韩志伟：男，副教授，研究方向为深度学习、图像处理

王惠：男，博士生，研究方向为强化学习、控制算法

洪玮佳：女，硕士生，研究方向为深度学习、图像处理

刘志刚：男，教授，研究方向为人工智能、深度学习

通讯作者:
韩志伟　zw.han@my.swjtu.edu.cn

中图分类号: TN922.3
计量
- 文章访问数: 21
- HTML全文浏览量: 10
- PDF下载量: 3
- 被引次数: 0
出版历程
- 收稿日期: 2025-04-30
- 修回日期: 2025-09-12
- 网络出版日期: 2025-09-16

Research on Active Control Strategies for High-speed Train Pantographs Based on Reinforcement Learning-guided Model Predictive Control Algorithms

School of Electric Engineering, Southwest Jiaotong University, Chengdu 611756, China

摘要

摘要: 受电弓-接触网系统的耦合性能是影响高速列车受流稳定性和整体运行效率的关键因素。该文旨在提出一种能应对复杂工况的主动控制策略，以降低弓网接触力波动。然而，现有主流方法各有瓶颈，如强化学习存在样本效率低、易陷入局部最优的问题，而模型预测控制则受限于短期优化视野。为融合二者优势，该文提出一种基于强化学习指导模型预测控制(RL-GMPC)的受电弓主动控制算法。首先，建立有限元弓网耦合模型，用于生成多工况弓网交互数据；其次，基于强化学习框架提出一种自适应潜在动力学模型，其从弓网交互数据中学习系统动力学世界模型，并基于时序差分思想训练状态价值函数；进一步，提出一种基于强化学习指导的模型预测控制框架，其在滚动时域内使用学习的动力学模型进行局部轨迹优化，并使用学习的终端状态价值函数来估计轨迹末端状态的预期累计奖励。实现了短期累计奖励回报和长期奖励估计的有效结合。最后对算法进行了有效性测试和鲁棒性分析，实验结果表明，在京沪线运行条件下，基于RL-GMPC算法对受电弓进行主动控制，列车在290, 320, 350和380 km/h工况下的接触力标准差分别降低了14.29%, 18.07%, 21.52%和34.87%，有效抑制了接触力波动。另外，该文算法在面对随机风扰动及接触网线路参数变化时也表现出优异的鲁棒性。
- 高速铁路 /
- 受电弓主动控制 /
- 强化学习 /
- 模型预测控制
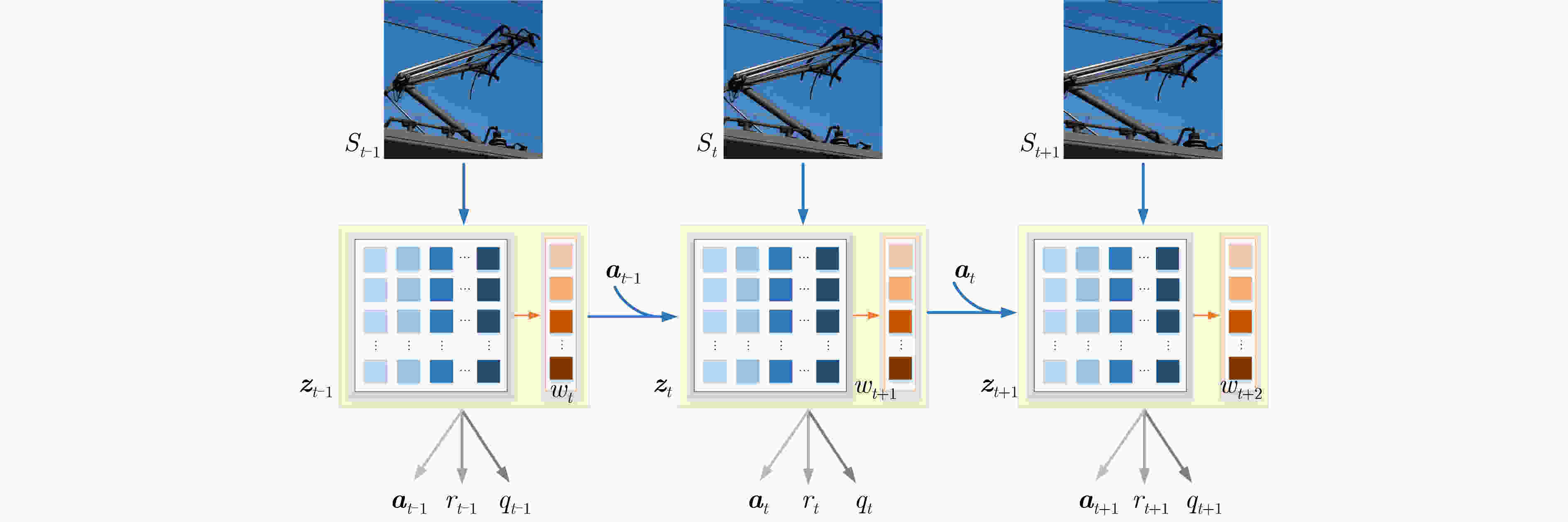
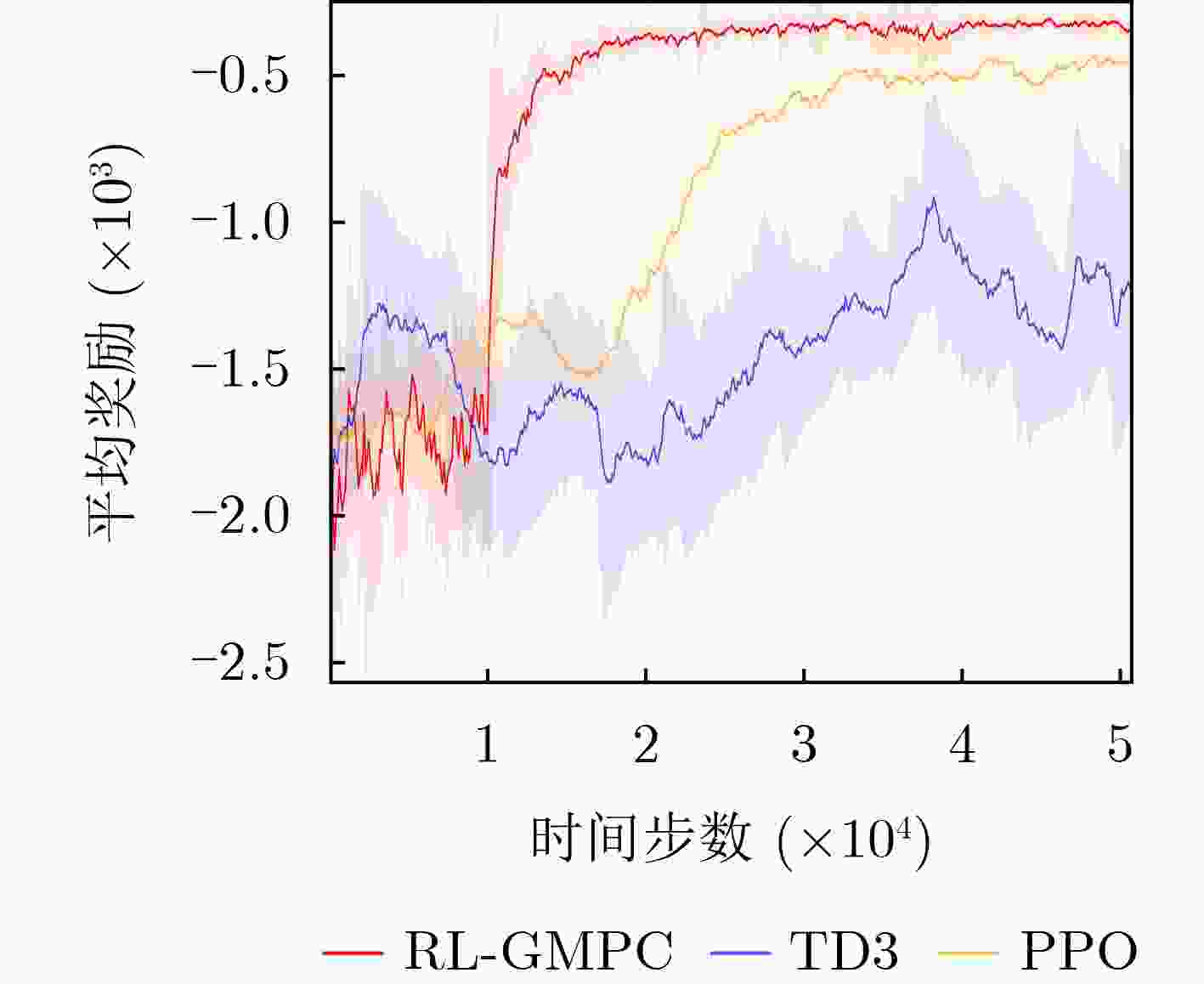
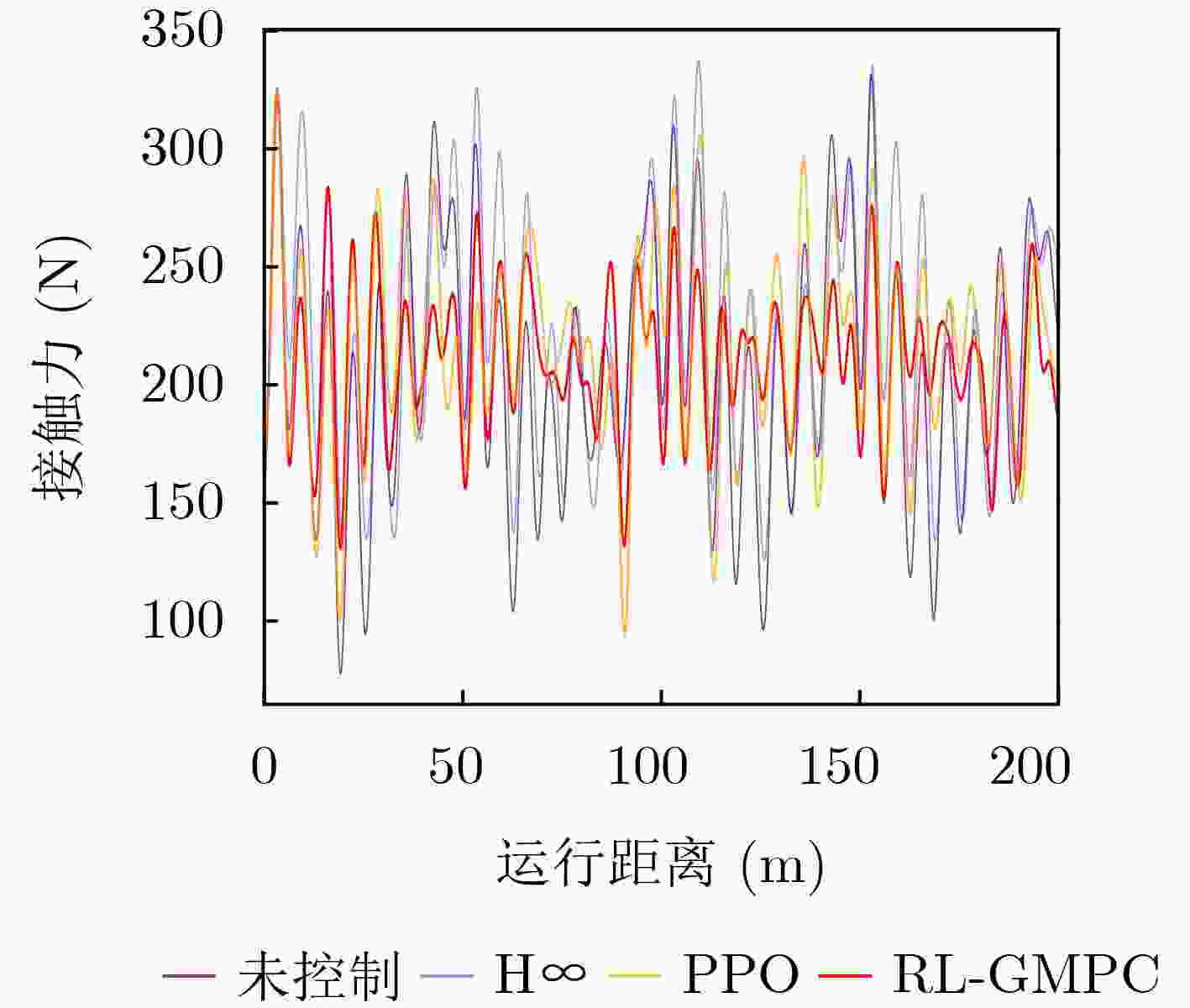
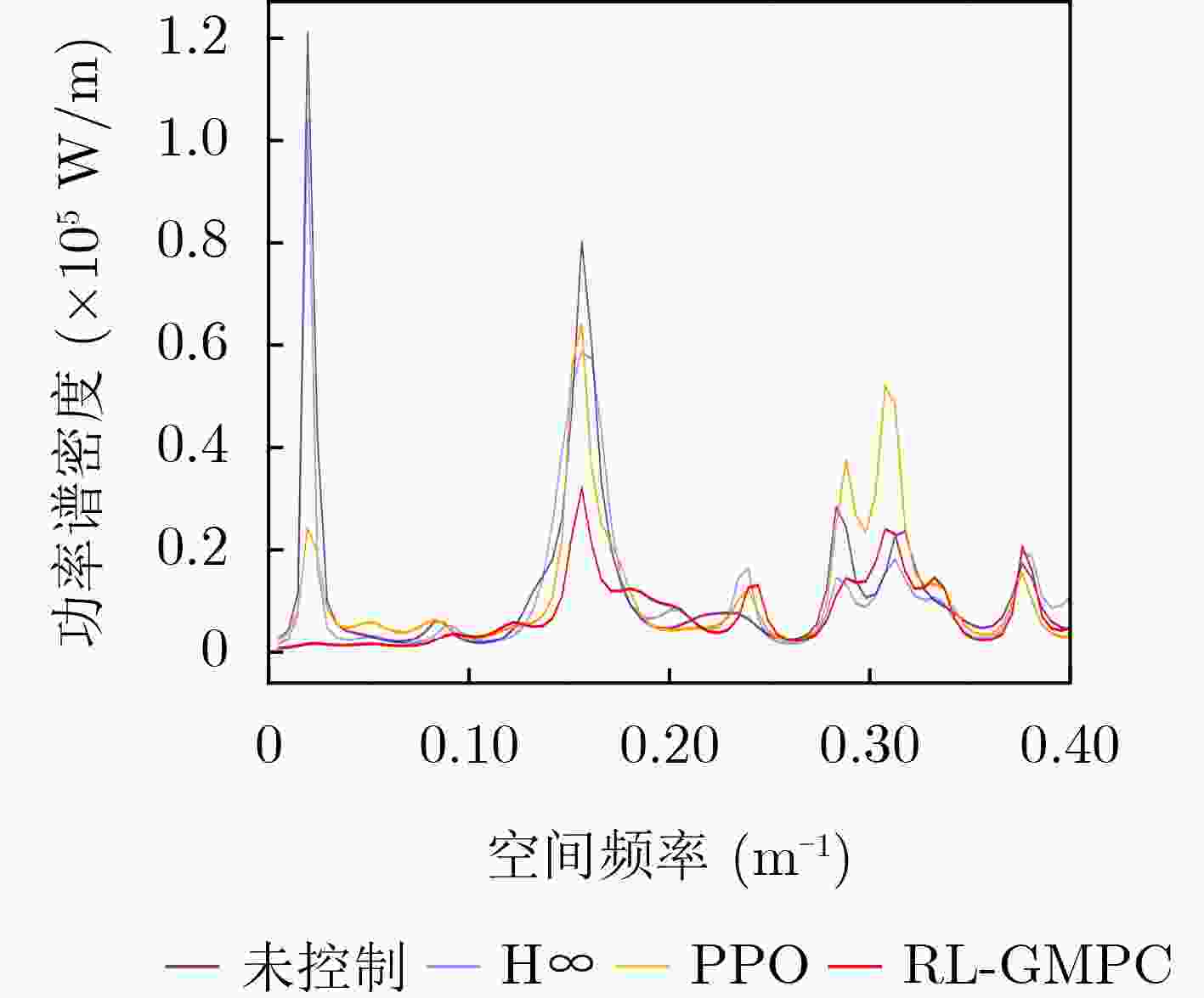
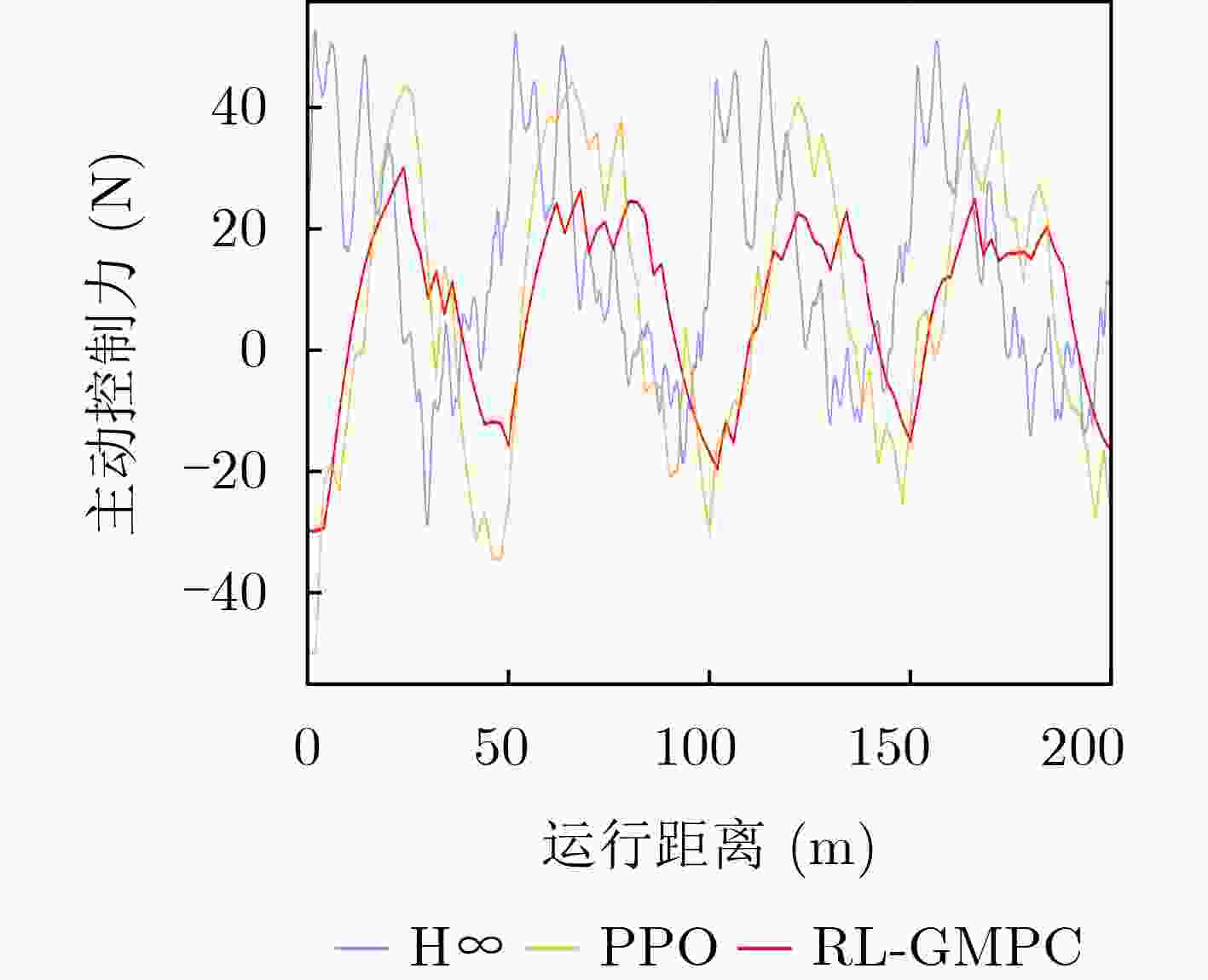
Abstract: Objective The coupled dynamics of the pantograph–catenary system are a critical determinant of current collection stability and the overall operational efficiency of high-speed trains. This study proposes an active control strategy that addresses complex operating conditions to mitigate fluctuations in pantograph–catenary contact force. Conventional approaches face inherent limitations: model-free Reinforcement Learning (RL) suffers from low sample efficiency and a tendency to converge to local optima, while Model Predictive Control (MPC) is constrained by its short optimization horizon. To integrate their complementary advantages, this paper develops a Reinforcement Learning-guided Model Predictive Control (RL-GMPC) algorithm for active pantograph control. The objective is to design a controller that combines the long-term planning capability of RL with the online optimization and constraint-handling features of MPC. This hybrid framework is intended to overcome the challenges of sample inefficiency, short-sighted planning, and limited adaptability, thereby achieving improved suppression of contact force fluctuations across diverse operating speeds and environmental disturbances. Methods A finite element model of the pantograph–catenary system is established, in which a simplified three-mass pantograph model is integrated with nonlinear catenary components to simulate dynamic interactions. The reinforcement learning framework is designed with an adaptive latent dynamics model to capture system behavior and a robust reward estimation module to normalize multi-scale rewards. The RL-GMPC algorithm is formulated by combining MPC for short-term trajectory optimization with a terminal state value function for estimating long-term cumulative rewards, thus balancing immediate and future performance. A Markov decision process environment is constructed by defining the state variables (pantograph displacement, velocity, acceleration, and contact force), the action space (pneumatic lift force adjustment), and the reward function, which penalizes contact force deviations and abrupt control changes. Results and Discussions Experimental validation under Beijing–Shanghai line conditions demonstrates significant reductions in contact force standard deviations: 14.29%, 18.07%, 21.52%, and 34.87% at 290, 320, 350, and 380 km/h, respectively. The RL-GMPC algorithm outperforms conventional H∞ control and Proximal Policy Optimization (PPO) by generating smoother control inputs and suppressing high-frequency oscillations. Robustness tests under 20% random wind disturbances show a 30.17% reduction in contact force variations, confirming adaptability to dynamic perturbations. Cross-validation with different catenary configurations (Beijing–Guangzhou and Beijing–Tianjin lines) reveals consistent performance improvements, with deviations reduced by 19.31%–33.62% across speed profiles. Training efficiency analysis indicates that RL-GMPC requires 57% fewer interaction samples than PPO to achieve convergence, demonstrating superior sample efficiency. Conclusions The RL-GMPC algorithm integrates the predictive capabilities of model-based control with the adaptive learning strengths of reinforcement learning. By dynamically optimizing pantograph posture, it enhances contact stability across varying speeds and environmental disturbances. Its demonstrated robustness to parameter variations and external perturbations highlights its practical applicability in high-speed railway systems. This study establishes a novel framework for improving pantograph–catenary interaction quality, reducing maintenance costs, and advancing the development of next-generation high-speed trains.
- High-speed railway /
- Active pantograph control /
- Reinforcement Learning (RL) /
- Model Predictive Control (MPC)

HTML全文

图 1 受电弓归算质量模型

下载: 全尺寸图片幻灯片

图 2 接触网模型

下载: 全尺寸图片幻灯片

图 3 马尔可夫决策环境

下载: 全尺寸图片幻灯片

图 4 RL-GMPC网络结构图

下载: 全尺寸图片幻灯片

图 5 自适应潜在动力学模型

下载: 全尺寸图片幻灯片

图 6 不同强化学习算法奖励曲线对比

下载: 全尺寸图片幻灯片

图 7 380 km/h下不同算法控制下的接触力对比

下载: 全尺寸图片幻灯片

图 8 380km/h速度下接触力的功率谱密度对比

下载: 全尺寸图片幻灯片

图 9 接触力标准差对比图

下载: 全尺寸图片幻灯片

图 10 不同算法下的主动控制力

下载: 全尺寸图片幻灯片

图 11 380km/h下加入20%噪声扰动前后对比图

下载: 全尺寸图片幻灯片

1 RL-GMPC伪代码

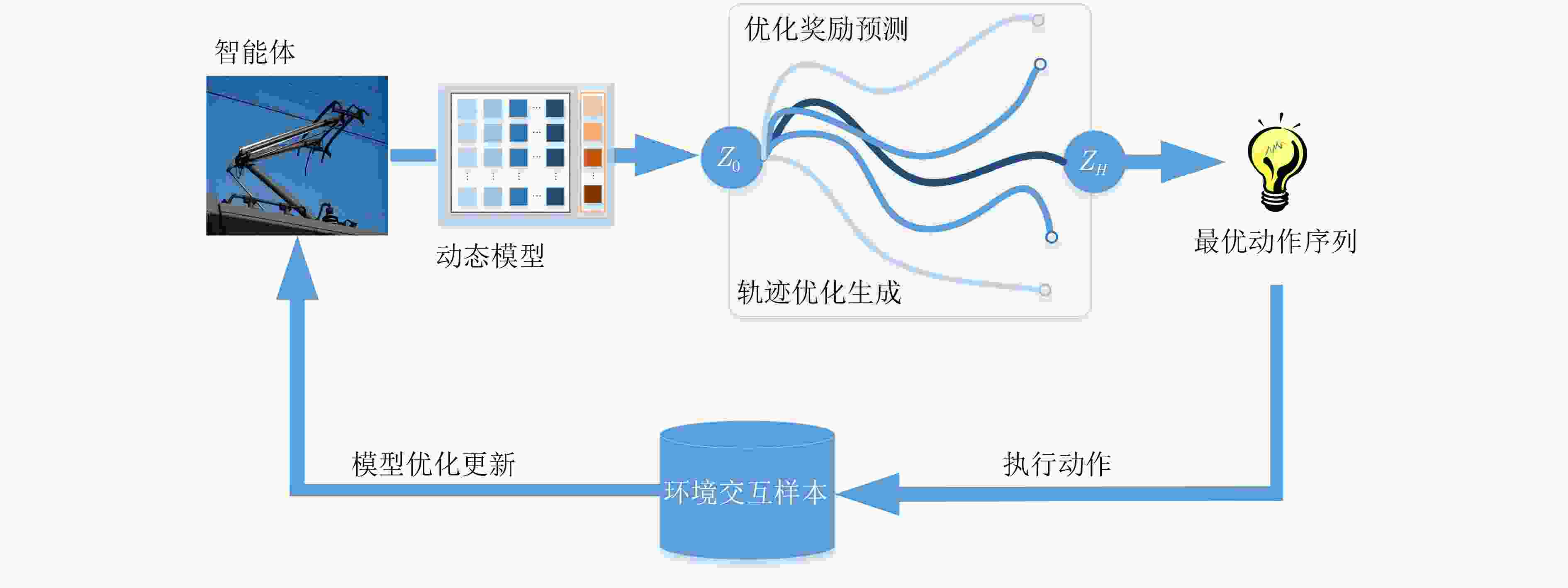
初始化：
初始化优化器和网络参数，设置超参数
${\mu ^0},{\sigma ^0}$：动作分布参数
$N,{N_\pi }$：轨迹采样数
$H,J$：规划时域长度、规划迭代次数
初始化经验回放缓冲区Buffer，环境Env
编码状态：${z_t} = {h_\theta }({s_t})$
for $j = 1,2,\cdots,k$ do
从$\mathcal{N}$采样N条长度为H的动作序列
使用$ {p_\phi } $,$ {d_\phi } $生成${N_\pi }$条长度H的路径
//初始化路径回报，使用自适应动态、鲁棒奖励和价值
对于$({a_t},{a_{t + 1}}, \cdots ,{a_{t + H}})$，做如下动态权重调整
${w_t} \leftarrow {\mathcal{L}_w}({z_t},{s_t})$，如式(18) //适应潜在动态 (ALD)
for $ t = 0 ,1,\cdots, H - 1 $ do
${\phi ^r} \leftarrow {\phi ^r} + {R_\theta }({z_{\text{t}}},{a_{\text{t}}})$ //鲁棒奖励 (RRE)
$ {z_{t + 1}} \leftarrow {d_q}({z_t},{a_t},{w_t}) $ //动态潜在转移
${\phi ^r} \leftarrow {\phi ^r} + \lambda {Q_T}({z_t},{a_t})$ //累加终端价值
调整回报权重$ \leftarrow {{\mathrm{normalize}}\_{\mathrm{returns}}}{\text{(}}{\phi ^r})$
基于$N + {N_\pi }$条轨迹回报对参数$\mu ,\sigma $进行更新
$\mu ,\sigma $$ \leftarrow $适应性加权调整(基于优化回报${\phi ^r}$)
返回$\mathcal{N}\left( {\mu ,{\sigma ^2}} \right)$ //使用ETO优化

下载: 导出CSV

表 1 RL-GMPC算法超参数设置

参数	数值	参数	数值
经验缓冲区	10 000	折扣因子$\lambda $	0.95～0.99
规划视野长度H	3	温度系数$\tau $	0.5
迭代次数J	6	损失平衡系数	0.1
采样轨迹数量N	128	学习率	3e-4
采样轨迹长度H	3	批次大小	64
Q网络数量	3	目标网络更新率	0.01
最优轨迹样本数N_e	32	滚动优化步长	1

下载: 导出CSV

表 2 接触网结构参数

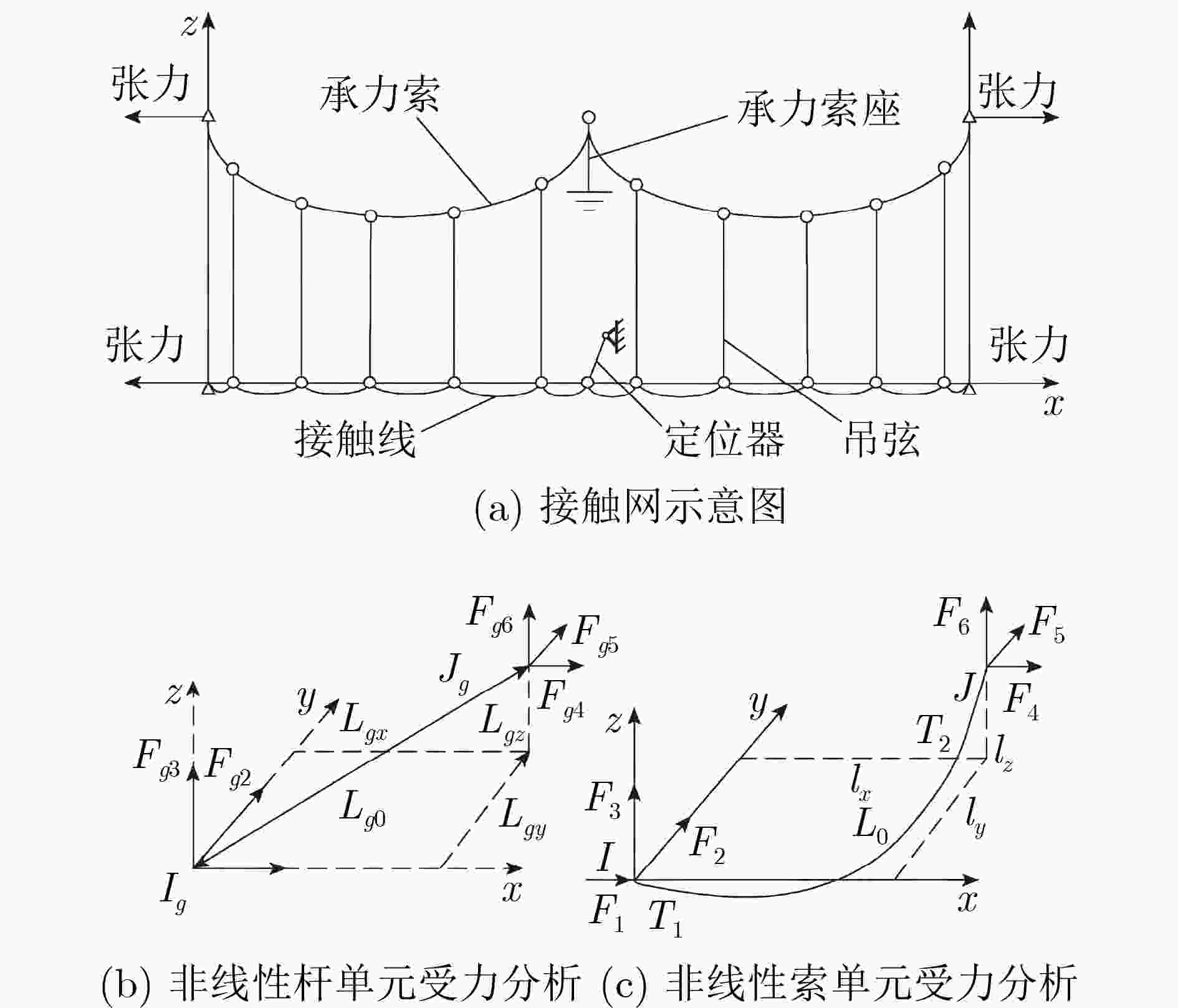
跨距(m)	结构高度(m)	承力索张力(N)	接触线张力(N)	承力索线密度/(kg/m)	接触线线密度/(kg/m)
50	1.6	20 000	33 000	1.065	1.35

下载: 导出CSV

表 3 受电弓结构参数

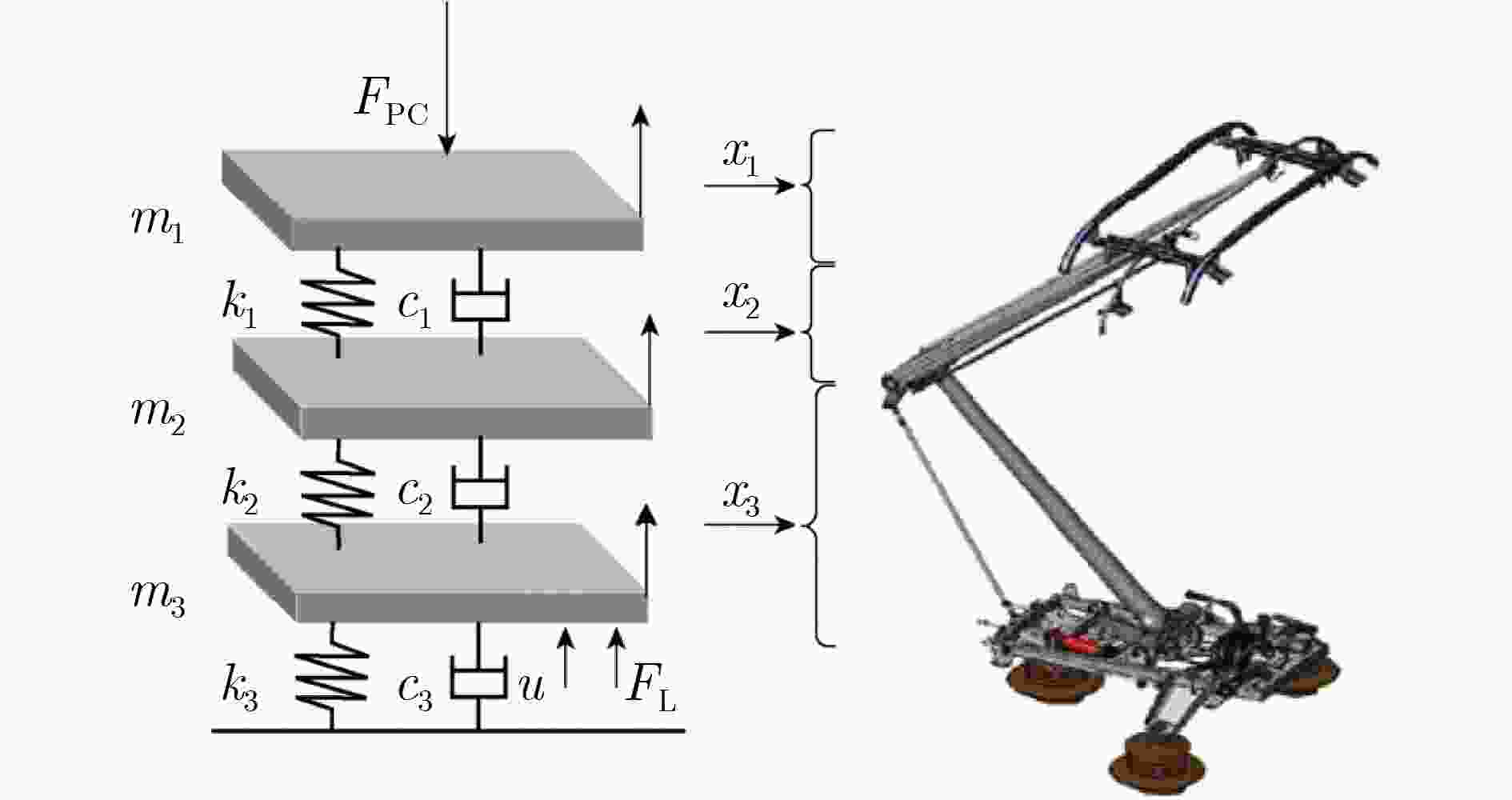
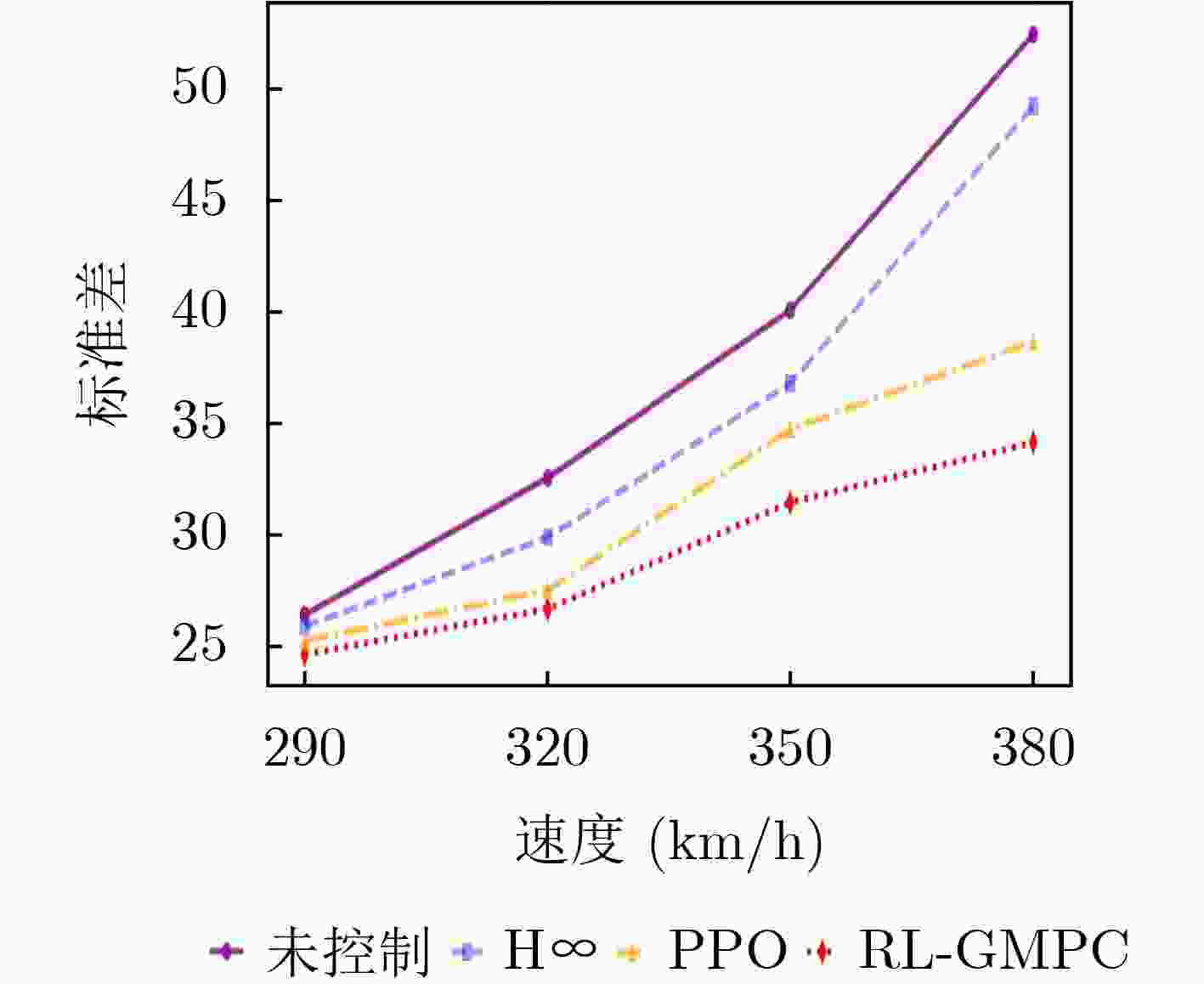
受电弓	型号	DSA380
等效质量(kg)	${m_{\text{1}}}$	7.12
	${m_{\text{2}}}$	6
	${m_{\text{3}}}$	5.8
等效阻尼(N·s/m)	${c_{\text{1}}}$	0
	${c_2}$	0
	${c_3}$	70
等效刚度(N/m)	${k_{\text{1}}}$	9 340
	${k_2}$	14 100
	${k_3}$	0.1

下载: 导出CSV

表 4 不同算法下接触力标准差对比

速度(km/h)	未控制标准差	H∞	PPO	RL-GMPC
290	26.45	25.93	24.58	22.67(14.29%)
320	32.60	29.93	27.56	26.71(18.07%)
350	40.11	36.82	34.76	31.48(21.52%)
380	52.48	49.26	38.71	34.18(34.87%)

下载: 导出CSV

表 5 不同控制算法的性能与计算开销对比

参数	H∞	PPO	RL-GMPC
接触力标准差	49.26	38.71	34.18
单步推理时间	< 1 ms	11 ms	23 ms
模型内存占用	< 1 MB	14 MB	39 MB
收敛所需样本数	N/A	5×10⁴	1.5 x 10⁴

下载: 导出CSV

表 6 380 km/h下不同控制策略接触力标准差对比

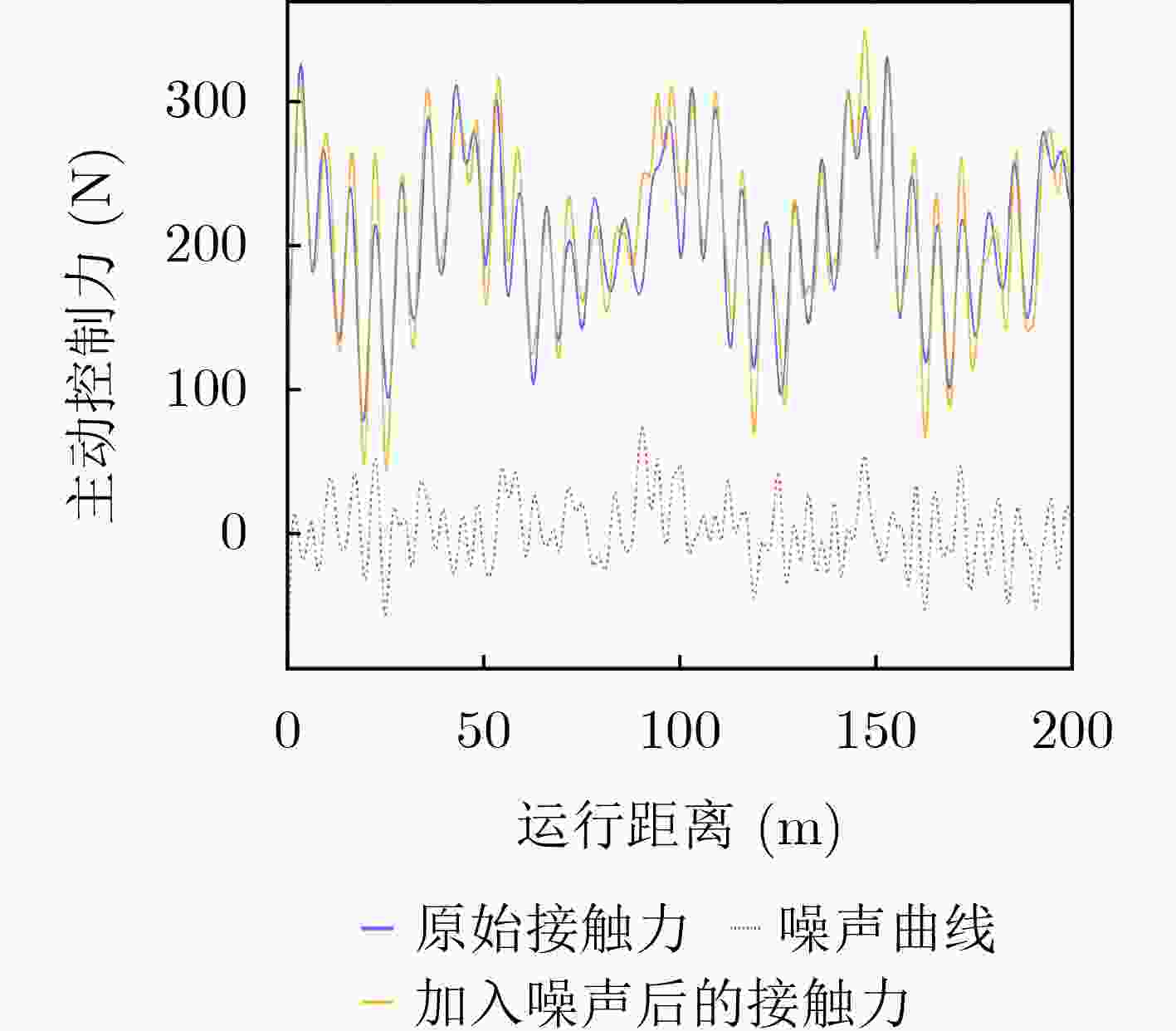
扰动强度(%)	未控制标准差	H∞	PPO	RL-GMPC
0	52.48	49.26	38.71	34.18(34.87%)
5	52.97	50.01	44.56	34.91(34.09%)
10	54.50	53.25	44.23	36.08(33.80%)
20	59.16	55.78	48.26	41.31(30.17%)

下载: 导出CSV

表 7 不同接触网配置下接触力标准差对比

线路	运行速度 (km/h)	标准差
线路	运行速度 (km/h)	未控	H∞	PPO	RL-GMPC
京沪线	320	32.60	29.93	27.56	26.71(18.07%)
	350	40.11	36.82	34.76	31.48(21.52%)
	380	52.48	49.26	38.71	34.18(34.87%)
京广线	320	30.09	27.07	25.48	24.28(19.31%)
	350	39.89	36.14	33,94	30.94(22.44%)
	380	50.04	48.39	38.06	33.63(32.79%)
京津线	320	32.34	29.34	28.10	26.83(17.04%)
	350	40.21	35.79	35.07	31.82(20.87%)
	380	51.43	48.82	39.73	34.14(33.62%)

下载: 导出CSV

参考文献(22)

[1]	余卫国, 熊幼京, 周新风, 等. 电力网技术线损分析及降损对策[J]. 电网技术, 2006, 30(18): 54–57,63. doi: 10.3321/j.issn:1000-3673.2006.18.011. YU Weiguo, XIONG Youjing, ZHOU Xinfeng, et al. Analysis on technical line losses of power grids and countermeasures to reduce line losses[J]. Power System Technology, 2006, 30(18): 54–57,63. doi: 10.3321/j.issn:1000-3673.2006.18.011.
[2]	吴延波, 韩志伟, 王惠, 等. 基于双延迟深度确定性策略梯度的受电弓主动控制[J]. 电工技术学报, 2024, 39(14): 4547–4556. doi: 10.19595/j.cnki.1000-6753.tces.230694. WU Yanbo, HAN Zhiwei, WANG Hui, et al. Active pantograph control of deep reinforcement learning based on double delay depth deterministic strategy gradient[J]. Transactions of China Electrotechnical Society, 2024, 39(14): 4547–4556. doi: 10.19595/j.cnki.1000-6753.tces.230694.
[3]	葛超, 张嘉滨, 王蕾, 等. 基于模型预测控制的自动驾驶车辆轨迹规划[J]. 计算机应用, 2024, 44(6): 1959–1964. doi: 10.11772/j.issn.1001-9081.2023050725. GE Chao, ZHANG Jiabin, WANG Lei, et al. Trajectory planning for autonomous vehicles based on model predictive control[J]. Journal of Computer Applications, 2024, 44(6): 1959–1964. doi: 10.11772/j.issn.1001-9081.2023050725.
[4]	DULAC-ARNOLD G, LEVINE N, MANKOWITZ D J, et al. Challenges of real-world reinforcement learning[J]. Machine Learning, 2021, 110(9): 2419–2468. doi: 10.1007/s10994-021-05961-4.
[5]	GUESTRIN C, LAGOUDAKIS M G, and PARR R. Coordinated reinforcement learning[C]. Proceedings of the 19th International Conference on Machine Learning, San Francisco, USA, 2002: 227–234.
[6]	HEGER M. Consideration of risk in reinforcement learning[M]. COHEN W W and HIRSH H. Machine Learning Proceedings 1994: Proceedings of the Eleventh International Conference. New Brunswick, 1994: 105–111. doi: 10.1016/B978-1-55860-335-6.50021-0.
[7]	VENKAT A N, HISKENS I A, RAWLINGS J B, et al. Distributed MPC strategies with application to power system automatic generation control[J]. IEEE Transactions on Control Systems Technology, 2008, 16(6): 1192–1206. doi: 10.1109/TCST.2008.919414.
[8]	LORENZEN M, CANNON M, and ALLGÖWER F. Robust MPC with recursive model update[J]. Automatica, 2019, 103: 461–471. doi: 10.1016/j.automatica.2019.02.023.
[9]	LIMON D, ALVARADO I, ALAMO T, et al. MPC for tracking piecewise constant references for constrained linear systems[J]. Automatica, 2008, 44(9): 2382–2387. doi: 10.1016/j.automatica.2008.01.023.
[10]	INCREMONA G P, FERRARA A, and MAGNI L. MPC for robot manipulators with integral sliding modes generation[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(3): 1299–1307. doi: 10.1109/TMECH.2017.2674701.
[11]	SONG Yang, LIU Zhigang, WANG Hongrui, et al. Nonlinear modelling of high-speed catenary based on analytical expressions of cable and truss elements[J]. Vehicle System Dynamics, 2015, 53(10): 1455–1479. doi: 10.1080/00423114.2015.1051548.
[12]	SCHIEHLEN W, GUSE N, and SEIFRIED R. Multibody dynamics in computational mechanics and engineering applications[J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(41/43): 5509–5522. doi: 10.1016/j.cma.2005.04.024.
[13]	陈庆斌, 韩先国, 李猛, 等. 一种机构型牵制释放装置的动力学建模与分析[J]. 航天制造技术, 2024(6): 26–34. doi: 10.3969/j.issn.1674-5108.2024.06.005. CHEN Qingbin, HAN Xianguo, LI Meng, et al. Dynamic modeling and analysis of a mechanism-type holding release device[J]. Aerospace Manufacturing Technology, 2024(6): 26–34. doi: 10.3969/j.issn.1674-5108.2024.06.005.
[14]	戈宝军, 殷继伟, 陶大军, 等. 基于励磁与调速控制的单机无穷大系统场-路-网时步有限元建模[J]. 电工技术学报, 2017, 32(3): 139–148. doi: 10.19595/j.cnki.1000-6753.tces.2017.03.016. GE Baojun, YIN Jiwei, TAO Dajun, et al. Modeling of field-circuit-network coupled time-stepping finite element for one machine infinite bus system based on excitation and speed control[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 139–148. doi: 10.19595/j.cnki.1000-6753.tces.2017.03.016.
[15]	陈忠华, 平宇, 陈明阳, 等. 波动接触力下弓网载流摩擦力建模研究[J]. 电工技术学报, 2019, 34(7): 1434–1440. doi: 10.19595/j.cnki.1000-6753.tces.180212. CHEN Zhonghua, PING Yu, CHEN Mingyang, et al. Research on current-carrying friction modeling of pantograph- catenary under fluctuation contact pressure[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1434–1440. doi: 10.19595/j.cnki.1000-6753.tces.180212.
[16]	叶圣永, 王晓茹, 周曙, 等. 基于马尔可夫链蒙特卡罗方法的电力系统暂态稳定概率评估[J]. 电工技术学报, 2012, 27(6): 168–174. doi: 10.19595/j.cnki.1000-6753.tces.2012.06.025. YE Shengyong, WANG Xiaoru, ZHOU Shu, et al. Power system probabilistic transient stability assessment based on Markov chain Monte Carlo method[J]. Transactions of China Electrotechnical Society, 2012, 27(6): 168–174. doi: 10.19595/j.cnki.1000-6753.tces.2012.06.025.
[17]	梁骅旗, 陆畅. 基于改进模型预测转矩控制的高精度PMSM控制方法研究[J]. 计算机测量与控制, 2025, 33(2): 152–160. doi: 10.16526/j.cnki.11-4762/tp.2025.02.020. LIANG Huaqi and LU Chang. High precision PMSM control method for predictive torque control based on improved model[J]. Computer Measurement & Control, 2025, 33(2): 152–160. doi: 10.16526/j.cnki.11-4762/tp.2025.02.020.
[18]	WANG Hui, HAN Zhiwei, LIU Zhigang, et al. Deep reinforcement learning based active pantograph control strategy in high-speed railway[J]. IEEE Transactions on Vehicular Technology, 2023, 72(1): 227–238. doi: 10.1109/TVT.2022.3205452.
[19]	HAARNOJA T, ZHOU A, ABBEEL P, et al. Soft actor-critic: off-policy maximum entropy deep reinforcement learning with a stochastic actor[C]. Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 2018: 1861–1870.
[20]	HANSEN N, SU Hao, and WANG Xiaolong. TD-MPC2: scalable, robust world models for continuous control[J]. arXiv preprint arXiv: 2310.16828, 2023. doi: 10.48550/arXiv.2310.16828. (查阅网上资料,不确定类型及格式是否正确,请确认).
[21]	DEWEY D. Reinforcement learning and the reward engineering principle[C]. Proceedings of the AAAI Spring Symposium, 2014. (查阅网上资料, 未找到出版地和doi信息, 请确认).
[22]	KUBANEK J, SNYDER L H, and ABRAMS R A. Reward and punishment act as distinct factors in guiding behavior[J]. Cognition, 2015, 139: 154–167. doi: 10.1016/j.cognition.2015.03.005.