复杂地形MIMO雷达低仰角估计方法

王佳佳; 郭瑞; 刘旗; 张月; 陈曾平

doi:10.11999/JEIT250236

复杂地形MIMO雷达低仰角估计方法

doi: 10.11999/JEIT250236 cstr: 32379.14.JEIT250236

中山大学电子与通信工程学院深圳 518107

基金项目: 国家自然科学基金(U2133216)，广东省科技厅先进智能感知技术重点实验室科技规划项目(2023B1212060024)，广东省科技技术项目(2019ZT08X751)，深圳市科技计划资助(KQTD20190929172704911)

详细信息

作者简介:
王佳佳：女，硕士生，研究方向为阵列信号处理

郭瑞：男，副教授，研究方向为数字信号处理、新体制雷达

刘旗：男，博士生，研究方向为阵列信号处理

张月：男，副教授，研究方向为雷达信号处理、智能目标识别

陈曾平：男，教授，研究方向为空间态势感知、软件化雷达探测

通讯作者:
郭瑞　guor29@mail.sysu.edu.cn

中图分类号: TN958
计量
- 文章访问数: 30
- HTML全文浏览量: 12
- PDF下载量: 3
- 被引次数: 0
出版历程
- 收稿日期: 2025-04-07
- 修回日期: 2025-09-03
- 网络出版日期: 2025-09-09

Low Elevation Angle Estimation Method for MIMO Radar in Complex Terrain

School of Electronics and Communication Engineering, Sun Yat-sen University, Shenzhen 518107, China

Funds: the National Natural Science Foundation of China (U2133216), Science and Technology Planning Project of Key Laboratory of Advanced IntelliSense Technology, Guangdong Science and Technology Department (2023B1212060024), Guangdong Provincial Science and Technology Program (2019ZT08X751), Shenzhen Science and Technology Program (KQTD20190929172704911)

摘要

摘要: 针对复杂地形多输入多输出(MIMO)雷达低仰角估计算法存在的孔径利用效率与计算复杂度的矛盾问题，该文提出了一种张量框架下的两步估计方法。首先构建三维张量观测模型以完整保留信号的多维结构特征，通过高阶奇异值分解(HOSVD)得到张量信号子空间并对其去冗余。然后采用稀疏贝叶斯学习(SBL)方法快速确定目标仰角和多径角度的初始估计。最后根据初始值和完整的张量信号子空间，通过交替迭代广义多重信号分类法(GMUSIC)获得目标仰角的精确估计。该方法适用于复杂地形，并且完整利用了阵列孔径，在估计性能和计算复杂度之间实现了良好的平衡。仿真实验和实测数据验证了该方法的有效性。
- 低仰角估计 /
- 复杂地形 /
- MIMO雷达 /
- 交替迭代
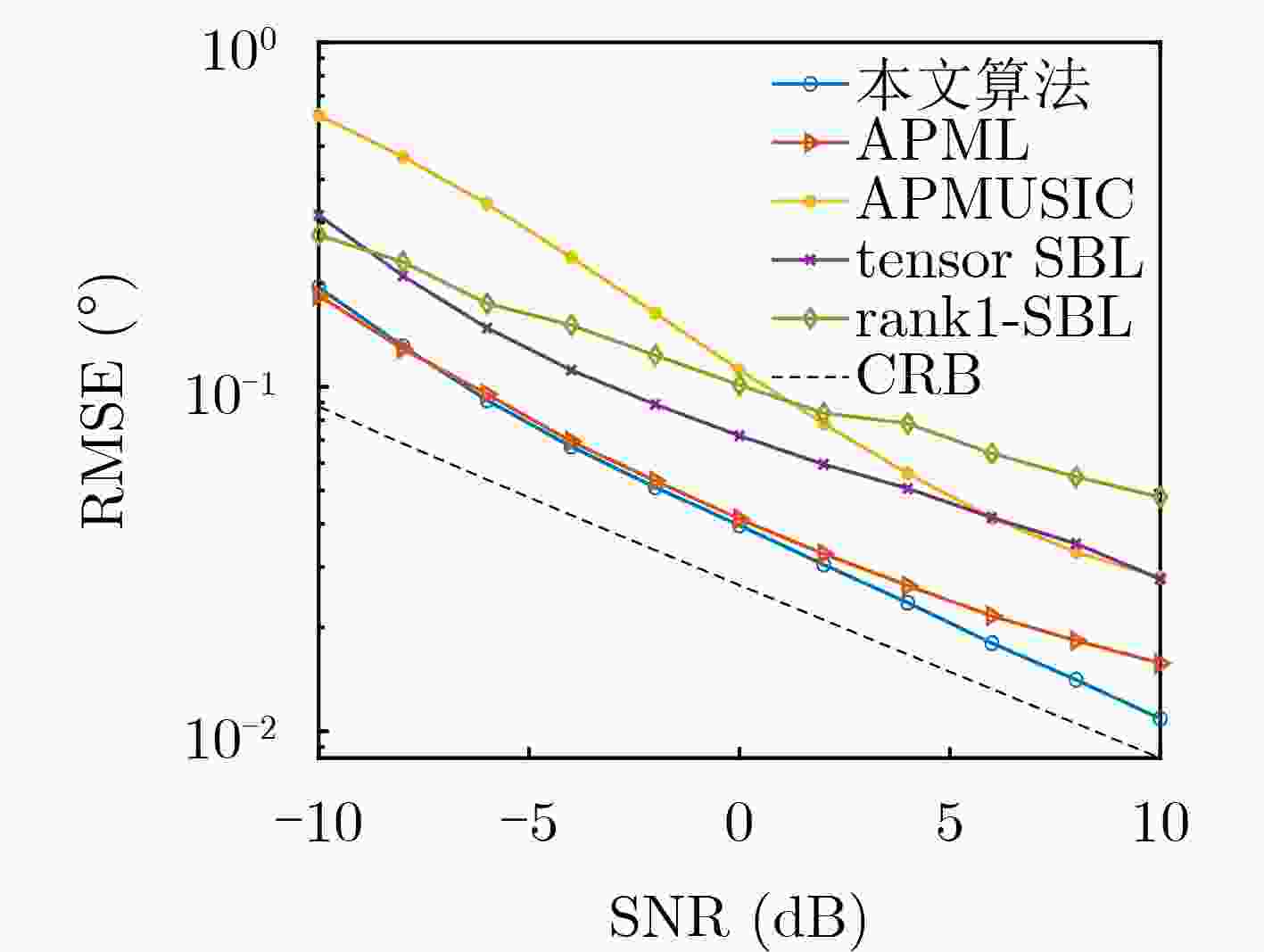
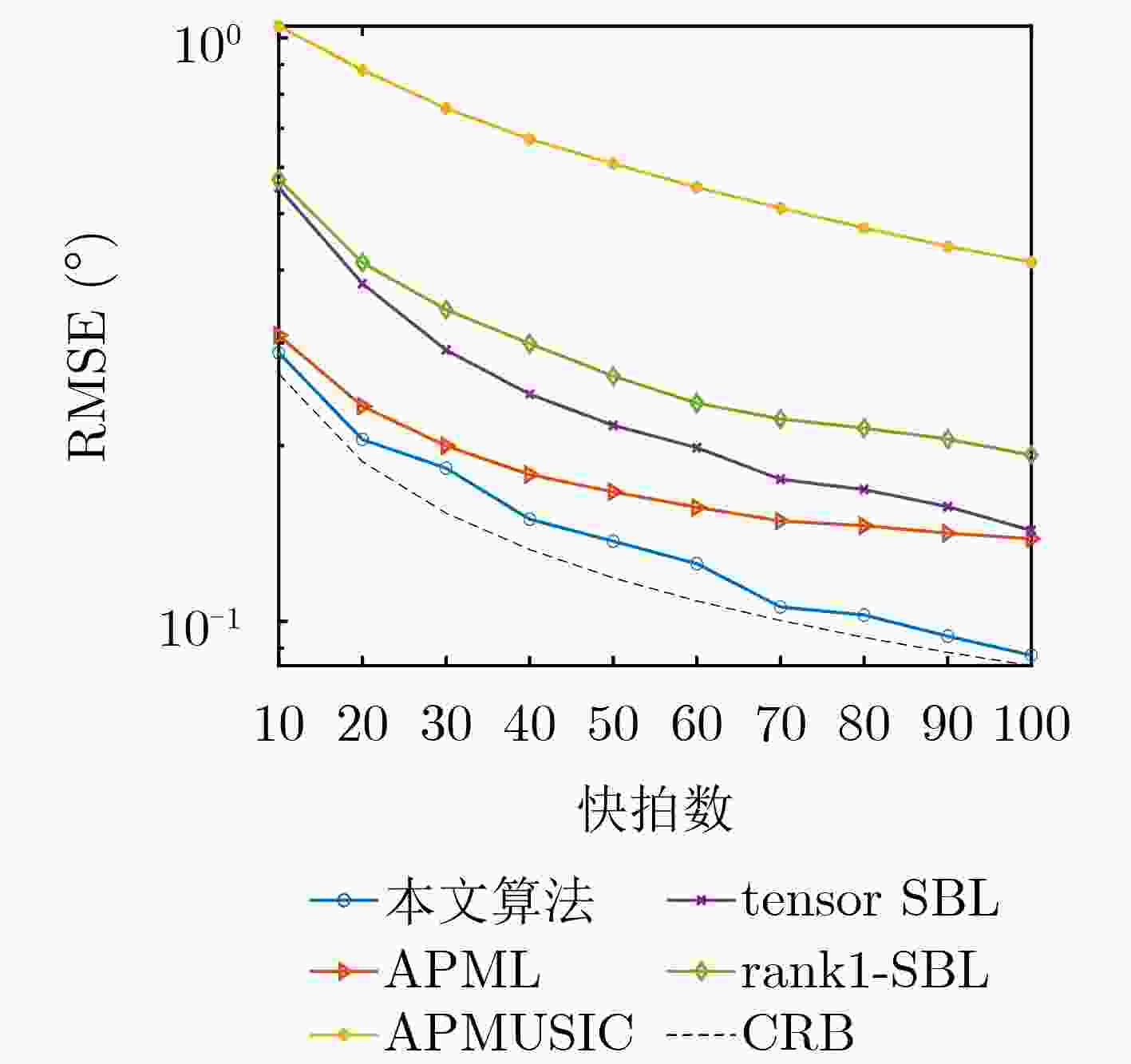
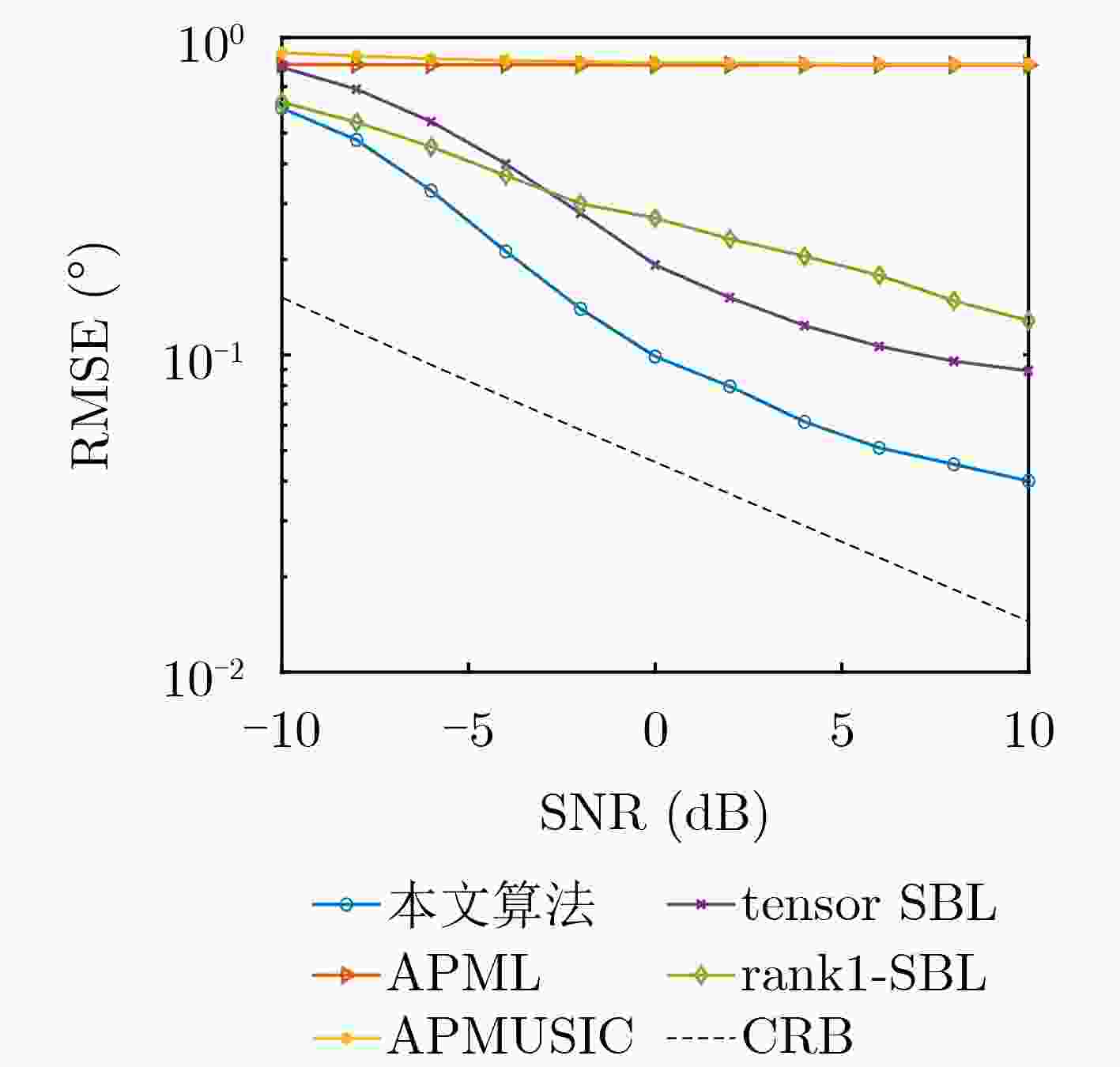
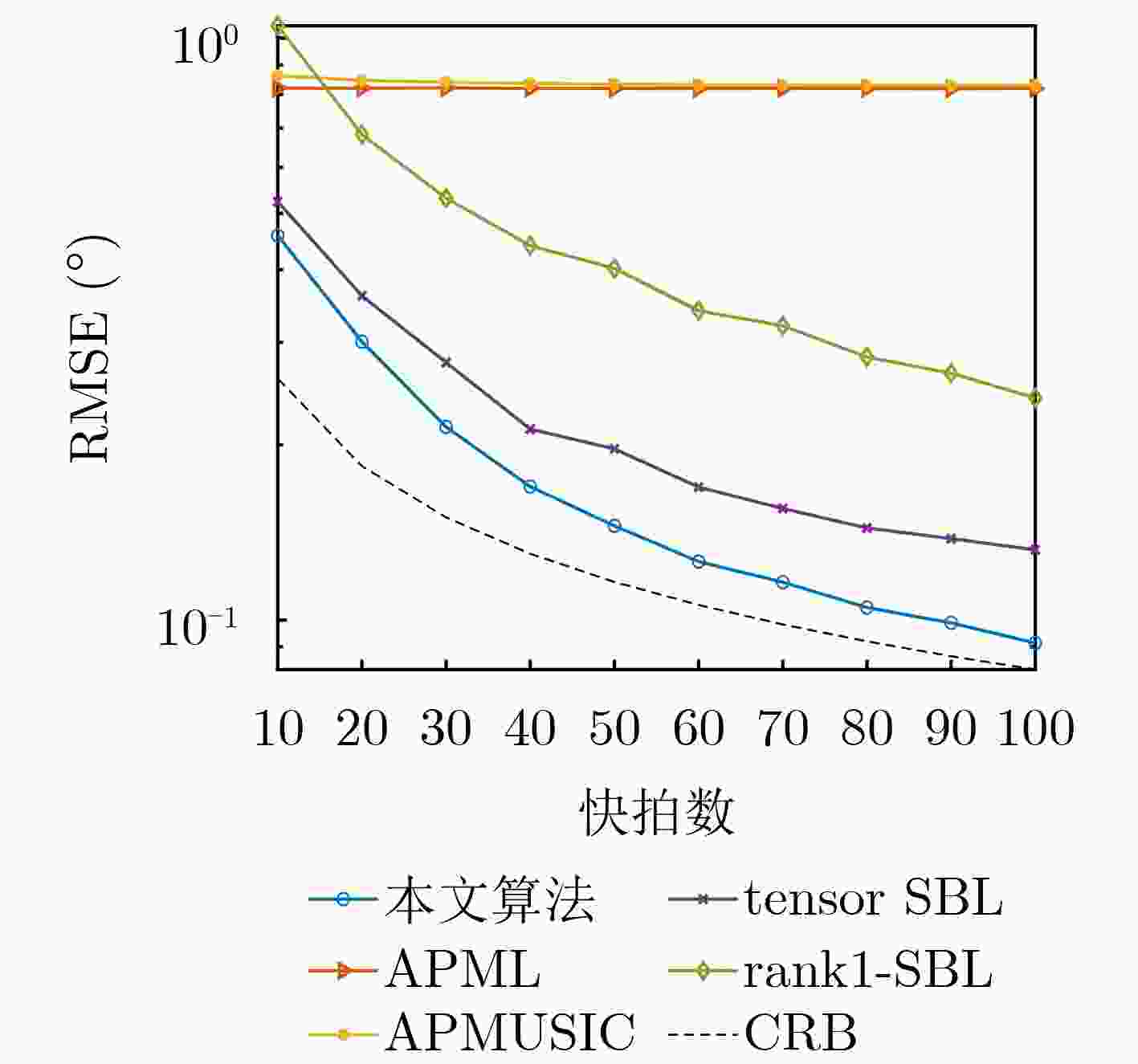
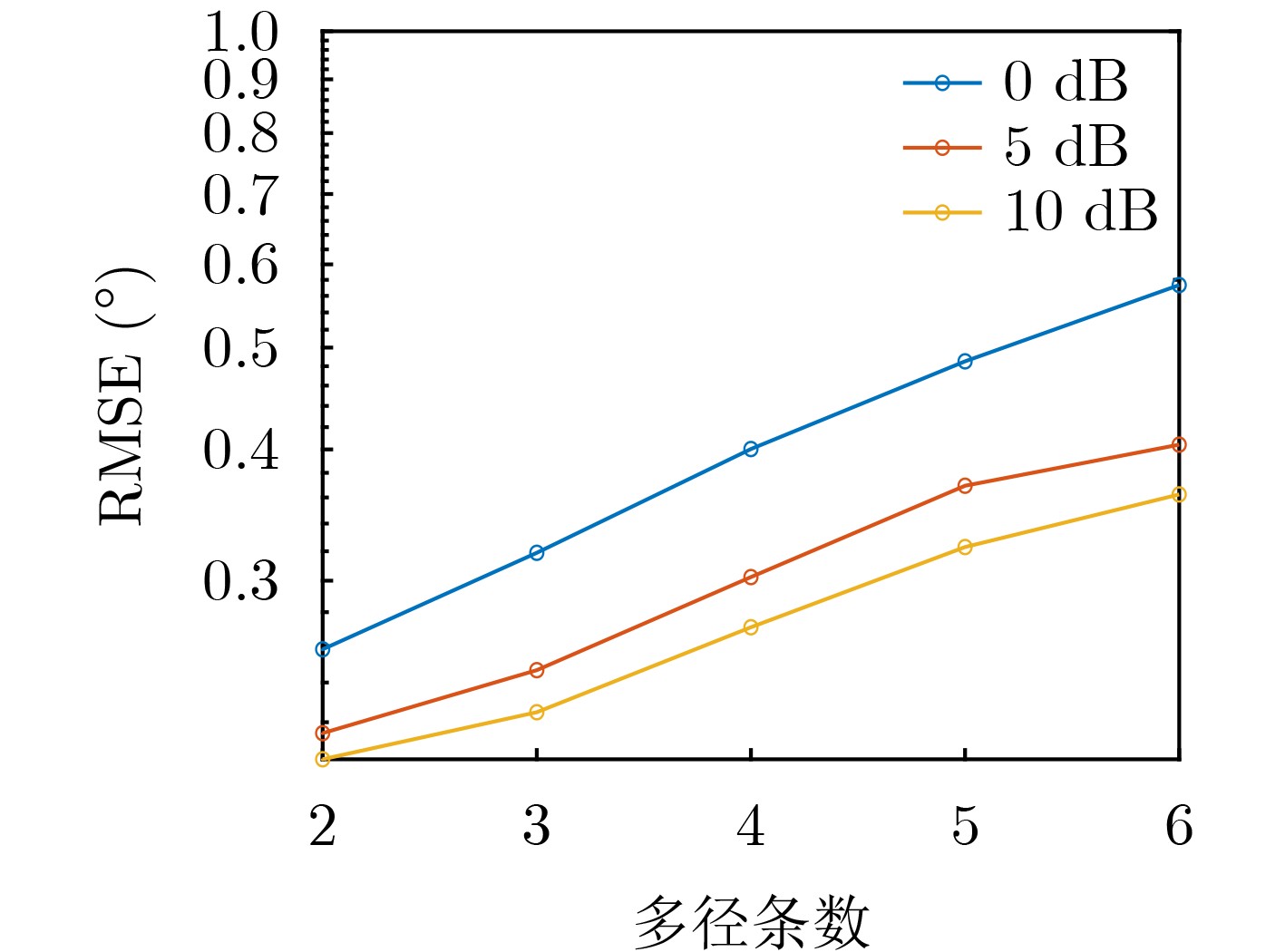
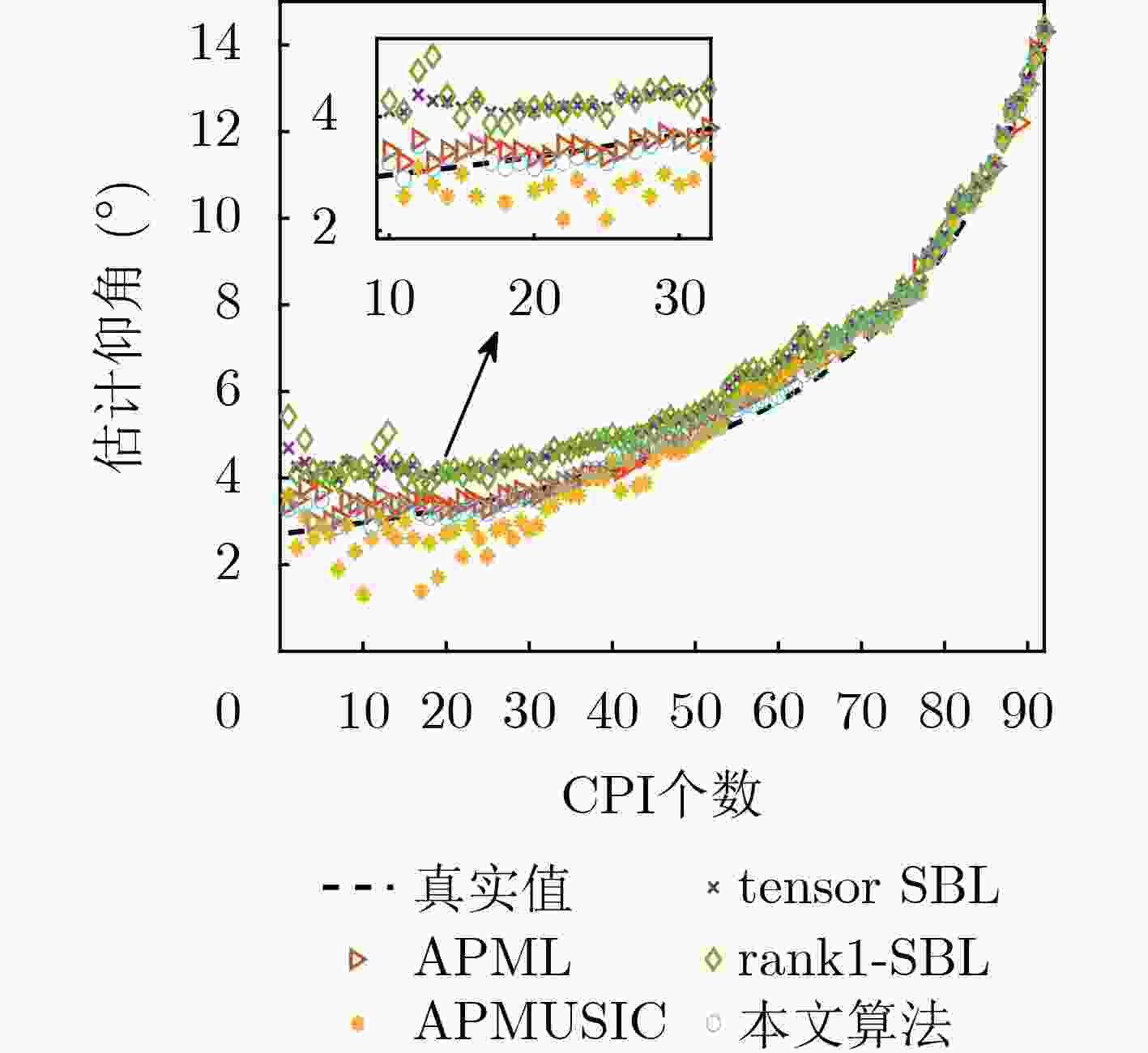
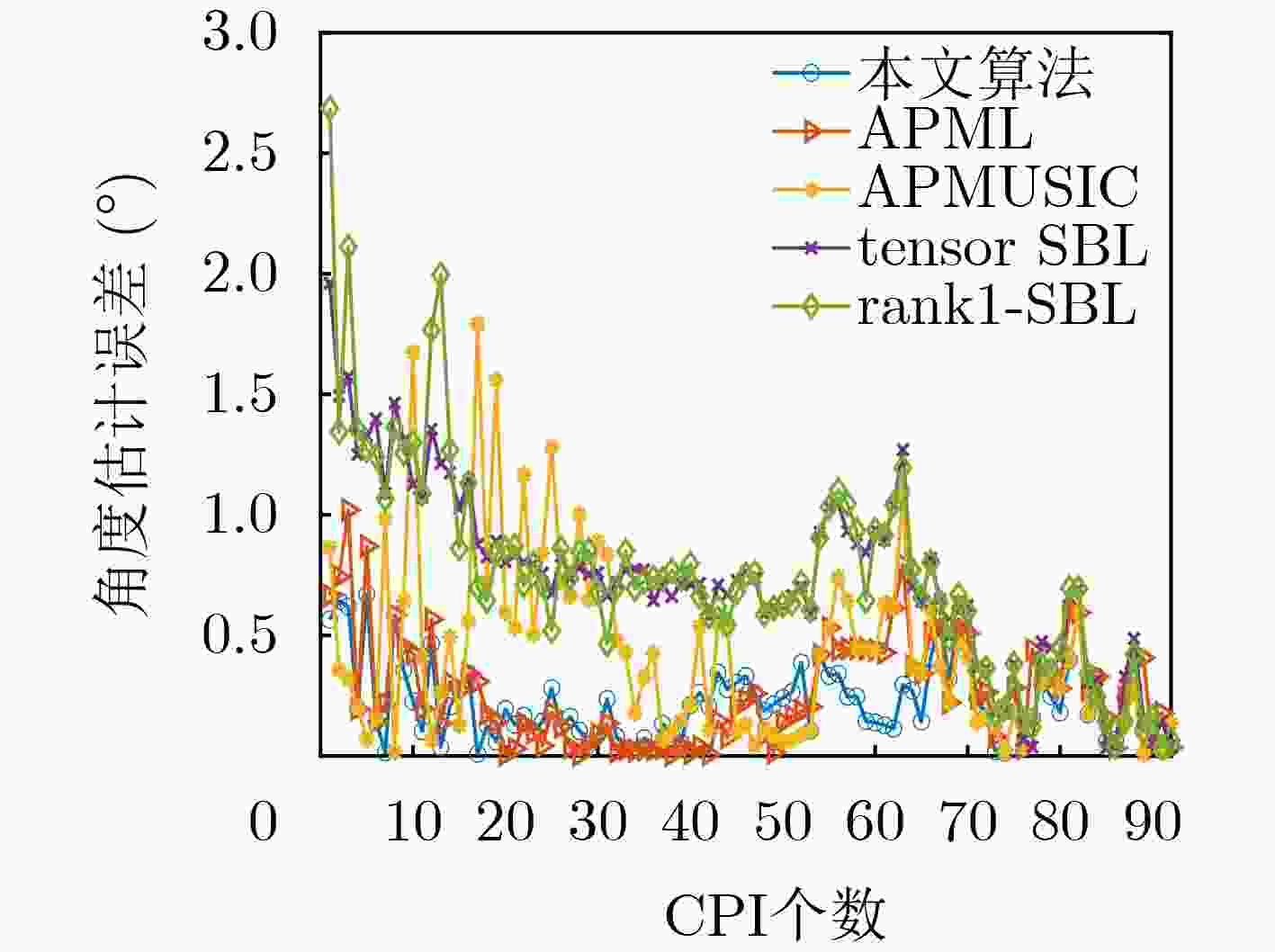
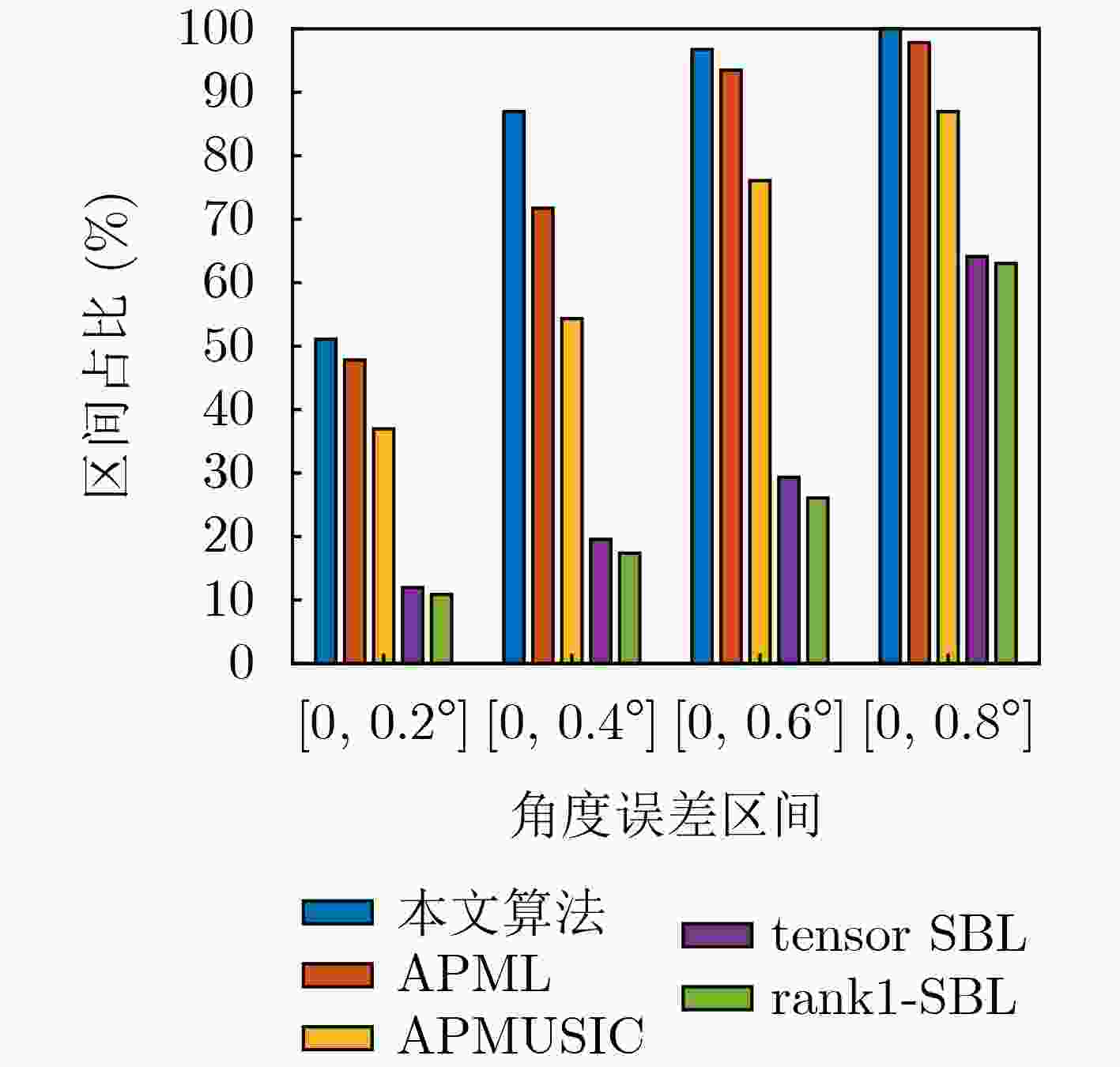
Abstract: Objective Conventional low-elevation angle estimation algorithms for Multiple-Input Multiple-Output (MIMO) radar generally assume a single-path propagation model, which limits their applicability in complex terrain where multipath effects are time-varying. Compressive Sensing (CS) algorithms exploit the sparsity of direct and multipath signals in the spatial domain and remain effective in such environments. Nonetheless, CS-based approaches for MIMO radar require the construction of a two-dimensional grid dictionary, and their computational complexity increases sharply as the number of multipath components grows. Existing complexity-reduction methods sacrifice array aperture, leading to degraded estimation accuracy. To resolve the trade-off between aperture utilization and computational complexity in low-elevation angle estimation for MIMO radar under complex terrain conditions, a tensor-based two-step estimation algorithm is proposed. Methods A three-dimensional tensor observation model is first established to fully preserve the multi-dimensional structure of the received signal, and the tensor signal subspace is extracted using High-Order Singular Value Decomposition (HOSVD). After eliminating redundancy in the tensor subspace, Sparse Bayesian Learning (SBL) is applied to rapidly obtain initial estimates of the low-elevation and multipath angles. These initial results are then refined by an alternating iterative Generalized Multiple Signal Classification (GMUSIC) algorithm, which leverages the complete tensor subspace. The proposed method maintains full array aperture, adapts to scenarios with unknown numbers of multipaths, and achieves a favorable balance between estimation accuracy and computational efficiency. Results and Discussions Simulation results demonstrate that the proposed algorithm achieves high estimation accuracy under both single- and double-reflection paths (Fig. 2–5) compared with other benchmark algorithms, while maintaining lower computational complexity (Table 1). Relative to the sub-optimal Alternative Projection Maximum Likelihood (APML) algorithm, the running speed is improved by 92.16%. In addition, the method remains robust under time-varying multipath conditions (Fig. 6) without requiring prior knowledge of the spatial distribution of reflection paths. Validation with real measured data (Fig. 8–10) further confirms its practical applicability: 86.95% of estimates fall within the 0–0.4° error range, and the error remains consistently below 0.6° across the observation window. These findings highlight the superior estimation accuracy and reliability of the proposed method, supporting its suitability for real-world engineering applications. Conclusions By integrating tensor modeling, sparse preliminary estimation, and alternating iterative optimization, the proposed algorithm fully exploits the multi-dimensional structure of the received signal and the complete array aperture of MIMO radar. It demonstrates high estimation accuracy while maintaining low computational complexity. Simulation results confirm its effectiveness and robustness in complex terrain, and validation with measured data further verifies its feasibility and engineering applicability. Nonetheless, this study is limited to a single-target scenario with a relatively simple motion trajectory. Future research should extend the method to address complex motion patterns with multiple targets.
- Low-elevation angle estimation /
- Complex terrain /
- Multiple-Input Multiple-Output (MIMO) radar /
- Alternating iteration

HTML全文

图 1 复杂地形单基地MIMO雷达多径传播模型

下载: 全尺寸图片幻灯片

图 2 RMSE随SNR的变化(单反射路径)

下载: 全尺寸图片幻灯片

图 3 RMSE随快拍数的变化(单反射路径)

下载: 全尺寸图片幻灯片

图 4 RMSE随SNR的变化(双反射路径)

下载: 全尺寸图片幻灯片

图 5 RMSE随快拍数的变化(双反射路径)

下载: 全尺寸图片幻灯片

图 6 RMSE随多径条数的变化

下载: 全尺寸图片幻灯片

图 7 实验场景

下载: 全尺寸图片幻灯片

图 8 估计仰角随CPI个数的变化

下载: 全尺寸图片幻灯片

图 9 估计误差随CPI个数的变化

下载: 全尺寸图片幻灯片

图 10 各算法估计误差在不同角度误差区间的占比

下载: 全尺寸图片幻灯片

表 1 SNR变化下5种算法的平均运行时间和计算复杂度

算法	搜索间隔(°)	平均耗时(s)	计算复杂度
本文算法	3.2节为0.10°，3.3节为0.01°	0.2769	$O\left\{ {{M^4} + {M^2}L + I\max (M{G^2},{M^3}) + \ell (8{M^4} + 24{M^2} + 147)} \right\}$
APML	0.01	3.5360	$O\left\{ {L{M^4} + \mu ({M^6} + 4{M^4} + 32{M^2} + 64)} \right\}$
APMUSIC	0.01	0.4568	$ O\left\{ {3{M^6} + (L + 4\mu + 4\mu F + 8F{H_{\text{p}}}){M^4} + (4\mu + 16F{H_{\text{p}}}){M^2}} \right\} $
tensor SBL	0.10	0.2189	$O\left\{ {{M^4} + {M^2}L + I\max (M{G^2},{M^3})} \right\}$
rank1-SBL	0.10	0.1559	$O\left\{ {{M^2}{L^2} + {M^3} + I\max (M{G^2},{M^3})} \right\}$

下载: 导出CSV

参考文献(28)

[1]	MA Jianjun, MA Hui, LIU Hongwei, et al. A novel DOA estimation for low-elevation target method based on multiscattering center equivalent model[J]. IEEE Geoscience and Remote Sensing Letters, 2023, 20: 3501605. doi: 10.1109/LGRS.2023.3242977.
[2]	LIU Qi, GUO Rui, WANG Bo, et al. Direct altitude estimation of low-elevation target for Bistatic holographic staring radar based on Coprime array[J]. IEEE Sensors Journal, 2024, 24(11): 17926–17940. doi: 10.1109/JSEN.2024.3387534.
[3]	PILLAI S U and KWON B H. Forward/backward spatial smoothing techniques for coherent signal identification[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(1): 8–15. doi: 10.1109/29.17496.
[4]	CADZOW J A, KIM Y S, and SHIUE D C. General direction-of-arrival estimation: A signal subspace approach[J]. IEEE Transactions on Aerospace and Electronic Systems, 1989, 25(1): 31–47. doi: 10.1109/7.18659.
[5]	ZOLTOWSKI M and HABER F. A vector space approach to direction finding in a coherent multipath environment[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(9): 1069–1079. doi: 10.1109/TAP.1986.1143956.
[6]	LIU Yuan, LIU Hongwei, XIA Xianggen, et al. Projection techniques for altitude estimation over complex multipath condition-based VHF radar[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(7): 2362–2375. doi: 10.1109/JSTARS.2018.2835448.
[7]	CHOI Y H. Alternating projection for maximum-likelihood source localization using eigendecomposition[J]. IEEE Signal Processing Letters, 1999, 6(4): 73–75. doi: 10.1109/97.752057.
[8]	BOSSE E, TURNER R M, and LECOURS M. Tracking swerling fluctuating targets at low altitude over the sea[J]. IEEE Transactions on Aerospace and Electronic Systems, 1991, 27(5): 806–822. doi: 10.1109/7.97326.
[9]	WU Jianqi, ZHU Wei, and CHEN Xiaobai. Compressed sensing techniques for altitude estimation in multipath conditions[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(3): 1891–1900. doi: 10.1109/TAES.2015.130841.
[10]	LIU Yuan, LIU Hongwei, WANG Lu, et al. Target localization in high-coherence multipath environment based on low-rank decomposition and sparse representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(9): 6197–6209. doi: 10.1109/TGRS.2020.2975218.
[11]	YANG Zai, LI Jian, STOICA P, et al. Sparse methods for direction-of-arrival estimation[M]. CHELLAPPA R and THEODORIDIS S. Academic Press Library in Signal Processing. Amsterdam: Elsevier, 2018: 509–581. doi: 10.1016/B978-0-12-811887-0.00011-0.
[12]	陈胜, 赵永波, 庞晓娇, 等. 米波MIMO雷达波束空间精确最大似然算法[J]. 系统工程与电子技术, 2022, 44(5): 1520–1526. doi: 10.12305/j.issn.1001-506X.2022.05.12. CHEN Sheng, ZHAO Yongbo, PANG Xiaojiao, et al. Beam space refined maximum likelihood algorithm for VHF MIMO radar[J]. Systems Engineering and Electronics, 2022, 44(5): 1520–1526. doi: 10.12305/j.issn.1001-506X.2022.05.12.
[13]	TANG Derui, ZHAO Yongbo, NIU Ben, et al. Bistatic MIMO radar height estimation method based on adaptive beam-space RML data fusion[J]. Digital Signal Processing, 2024, 145: 104346. doi: 10.1016/j.dsp.2023.104346.
[14]	CHEN Sheng, ZHAO Yongbo, and HU Yili. Beamspace phase solving algorithm for elevation angle estimation[J]. IEEE Signal Processing Letters, 2022, 29: 742–746. doi: 10.1109/LSP.2022.3154686.
[15]	SHI Junpeng, HU Guoping, ZHANG Xiaofei, et al. Sparsity-based DOA estimation of coherent and uncorrelated targets with flexible MIMO radar[J]. IEEE Transactions on Vehicular Technology, 2019, 68(6): 5835–5848. doi: 10.1109/TVT.2019.2913437.
[16]	LIU Yuan, JIU Bo, XIA Xianggen, et al. Height measurement of low-angle target using MIMO radar under multipath interference[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(2): 808–818. doi: 10.1109/TAES.2017.2767919.
[17]	TETI J G. Wide-band airborne radar operating considerations for low-altitude surveillance in the presence of specular multipath[J]. IEEE Transactions on Antennas and Propagation, 2000, 48(2): 176–191. doi: 10.1109/8.833067.
[18]	WANG Xianpeng, GUO Yuehao, WEN Fangping, et al. EMVS-MIMO radar with sparse Rx geometry: Tensor modeling and 2-D direction finding[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(6): 8062–8075. doi: 10.1109/TAES.2023.3297570.
[19]	SOKAL B, FAZAL-E-ASIM, and DE ALMEIDA A L F. Higher-order tensor-based joint transmit/receive beamforming and IRS optimization[C]. IEEE 9th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, Herradura, Costa Rica, 2023: 216–220, doi: 10.1109/CAMSAP58249.2023.10403475.
[20]	LIU Qi, WANG Xianpeng, HUANG Mengxing, et al. DOA and range estimation for FDA-MIMO radar with sparse Bayesian learning[J]. Remote Sensing, 2021, 13(13): 2553. doi: 10.3390/rs13132553.
[21]	YANG Zai, XIE Lihua, and ZHANG Cishen. Off-grid direction of arrival estimation using sparse Bayesian inference[J]. IEEE Transactions on Signal Processing, 2013, 61(1): 38–43. doi: 10.1109/TSP.2012.2222378.
[22]	王琦森, 余华, 李杰, 等. 基于稀疏贝叶斯学习的空间紧邻信号DOA估计算法[J]. 电子与信息学报, 2021, 43(3): 708–716. doi: 10.11999/JEIT200656. WANG Qisen, YU Hua, LI Jie, et al. Sparse Bayesian learning based algorithm for DOA estimation of closely spaced signals[J]. Journal of Electronics & Information Technology, 2021, 43(3): 708–716. doi: 10.11999/JEIT200656.
[23]	JIN Yi, HE Di, WEI Shuang, et al. Off-grid DOA estimation method based on sparse Bayesian learning with clustered structural-aware prior information[J]. IEEE Transactions on Vehicular Technology, 2024, 73(4): 5469–5483. doi: 10.1109/TVT.2023.3335959.
[24]	HUANG Chenglin, TIAN Zengshan, LIU Kaikai, et al. DoA estimation of nonuniform noise sources via off-grid SBL in a noncooperative mode using a single RF link[J]. IEEE Transactions on Microwave Theory and Techniques, 2025, 73(3): 1381–1395. doi: 10.1109/TMTT.2024.3464694.
[25]	张文俊, 赵永波, 张守宏. 广义MUSIC算法在米波雷达测高中的应用及其改进[J]. 电子与信息学报, 2007, 29(2): 387–390. doi: 10.3724/SP.J.1146.2005.00859. ZHANG Wenjun, ZHAO Yongbo, and ZHANG Shouhong. Altitude measurement of meter-wave radar using the general MUSIC algorithm and its improvement[J]. Journal of Electronics & Information Technology, 2007, 29(2): 387–390. doi: 10.3724/SP.J.1146.2005.00859.
[26]	ZHANG Yufeng, YE Zhongfu, and LIU Chao. Estimation of fading coefficients in the presence of multipath propagation[J]. IEEE Transactions on Antennas and Propagation, 2009, 57(7): 2220–2224. doi: 10.1109/TAP.2009.2021973.
[27]	TAN Jun and NIE Zaiping. Cramer-Rao bound of low angle estimation for VHF monostatic MIMO radar[C]. 2018 IEEE Radar Conference, Oklahoma City, USA, 2018: 158–163. doi: 10.1109/RADAR.2018.8378549.
[28]	郭瑞, 张月, 田彪, 等. 全息凝视雷达系统技术与发展应用综述[J]. 雷达学报, 2023, 12(2): 389–411. doi: 10.12000/JR22153. GUO Rui, ZHANG Yue, TIAN Biao, et al. Review of the technology, development and applications of holographic staring radar[J]. Journal of Radars, 2023, 12(2): 389–411. doi: 10.12000/JR22153.