无线传感网中的迭代加权最小二乘定位算法

闻建刚; 冯文淑; 冯晓斐; 华惊宇; 余绪涛

doi:10.11999/JEIT250203

无线传感网中的迭代加权最小二乘定位算法

doi: 10.11999/JEIT250203 cstr: 32379.14.JEIT250203

1.
浙江工商大学信息与电子工程学院杭州 310018
2.
东南大学移动信息与科学工程学院南京 210096

基金项目: 国家自然科学基金(62271445)

详细信息

作者简介:
闻建刚：男，讲师，博士，研究方向为无线通信中的信号处理

冯文淑：女，硕士生，研究方向为通信与网络

冯晓斐：女，副教授，硕士，研究方向为通信与网络

华惊宇：男，教授，博士，研究方向为无线定位、通信信号处理

余绪涛：女，教授，博士，研究方向为通信与网络

通讯作者:
华惊宇　eehjy@163.com

中图分类号: TN929.5
计量
- 文章访问数: 103
- HTML全文浏览量: 57
- PDF下载量: 18
- 被引次数: 0
出版历程
- 收稿日期: 2025-03-25
- 修回日期: 2025-05-29
- 网络出版日期: 2025-06-14
- 刊出日期: 2025-03-10

Iterative Weighted Least Square Localization Algorithm in Wireless Sensor Networks

1.
College of Information and Electronic Engineering, Zhejiang Gongshang University, Hangzhou 310018, China
2.
National Mobile Communication Research Laboratory, Southeast University, Nanjing 210096, China

Funds: The National Natural Science Foundation of China (62271445)

摘要

摘要: 物联网应用的快速发展，带来了对无线定位的广泛需求，但非视距(NLOS)传输环境对无线定位方法精度具有巨大影响。因此该文基于到达时间(TOA)测量与双静态节点组合定义了一种位置残差，并据此提出运用迭代加权最小二乘(IWLS)原理的无线定位算法。算法在当前WLS定位结果基础上，通过计算位置残差获得反映NLOS严重程度的权值向量，利用权值向量在下一次WLS估计中限制NLOS影响，产生更加精确的定位结果。在算法的执行过程中，残差-权值计算方式和NLOS测距数量都会影响定位性能，因此论文通过仿真分析了这些因素对于均方根误差(RMSE)和累计概率密度函数(CDF)的影响，确定了算法的最优参数设定。最后论文对比了IWLS算法和传统定位算法的性能，仿真结果表明，在典型非视距传输环境下，该文提出的IWLS算法性能优于传统算法。
- 无线定位 /
- 迭代加权最小二乘 /
- TOA /
- 位置残差 /
- 非视距误差
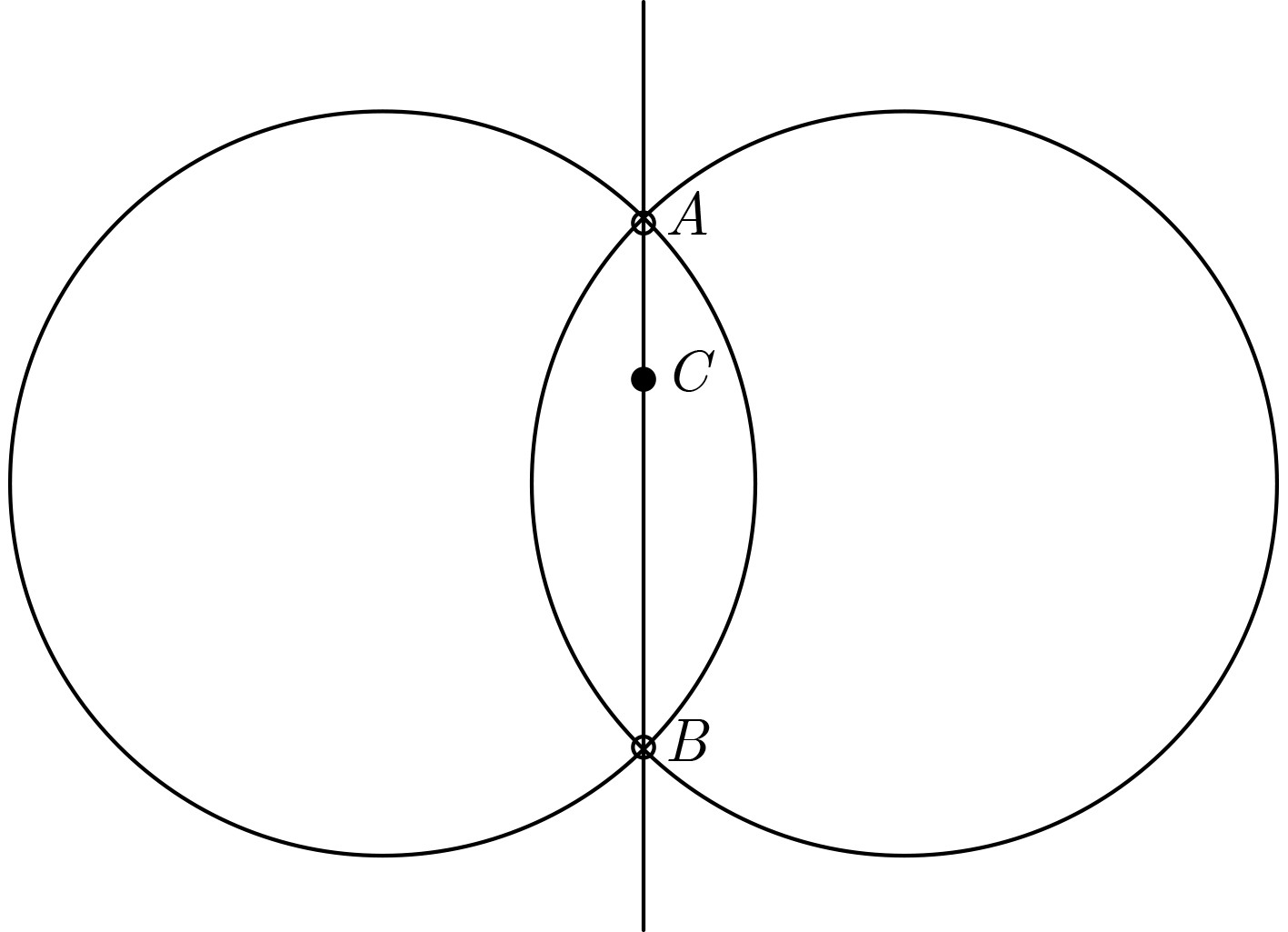
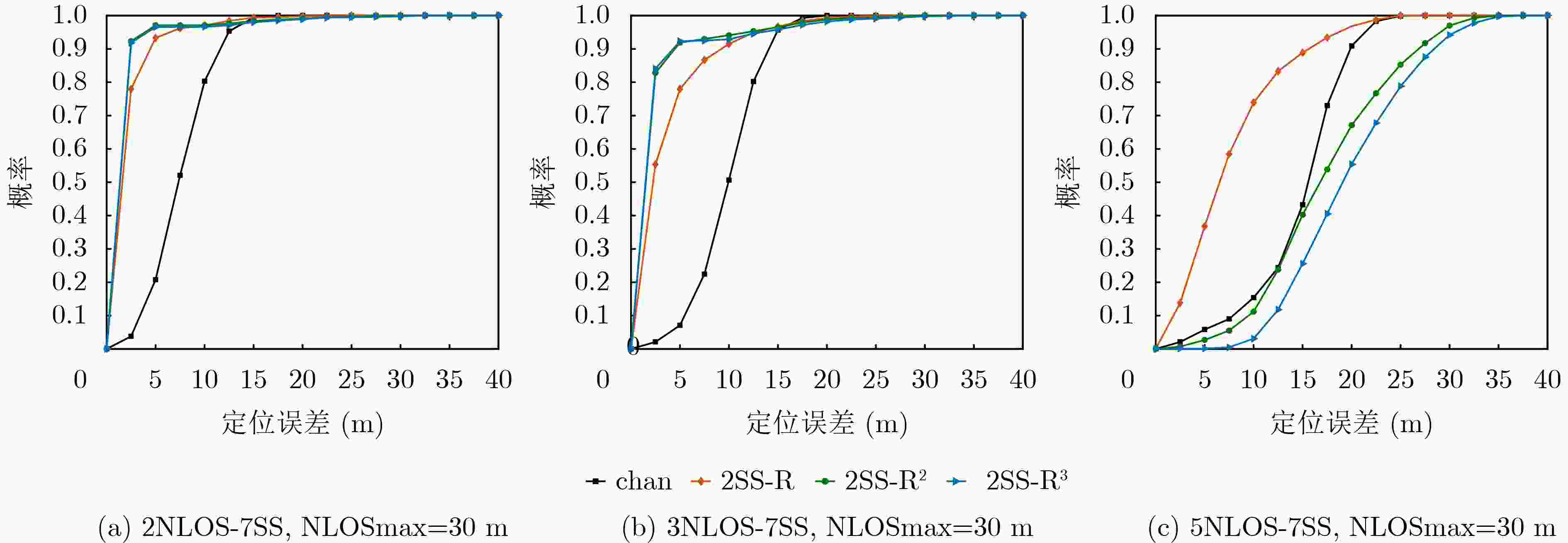
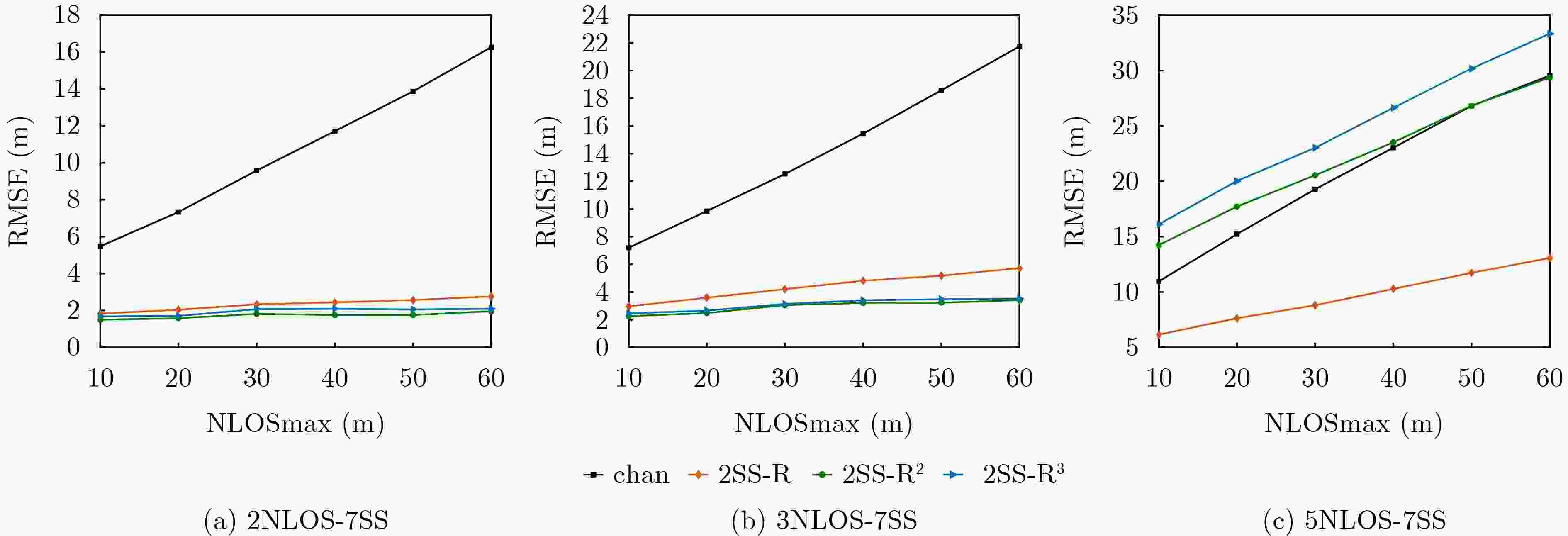
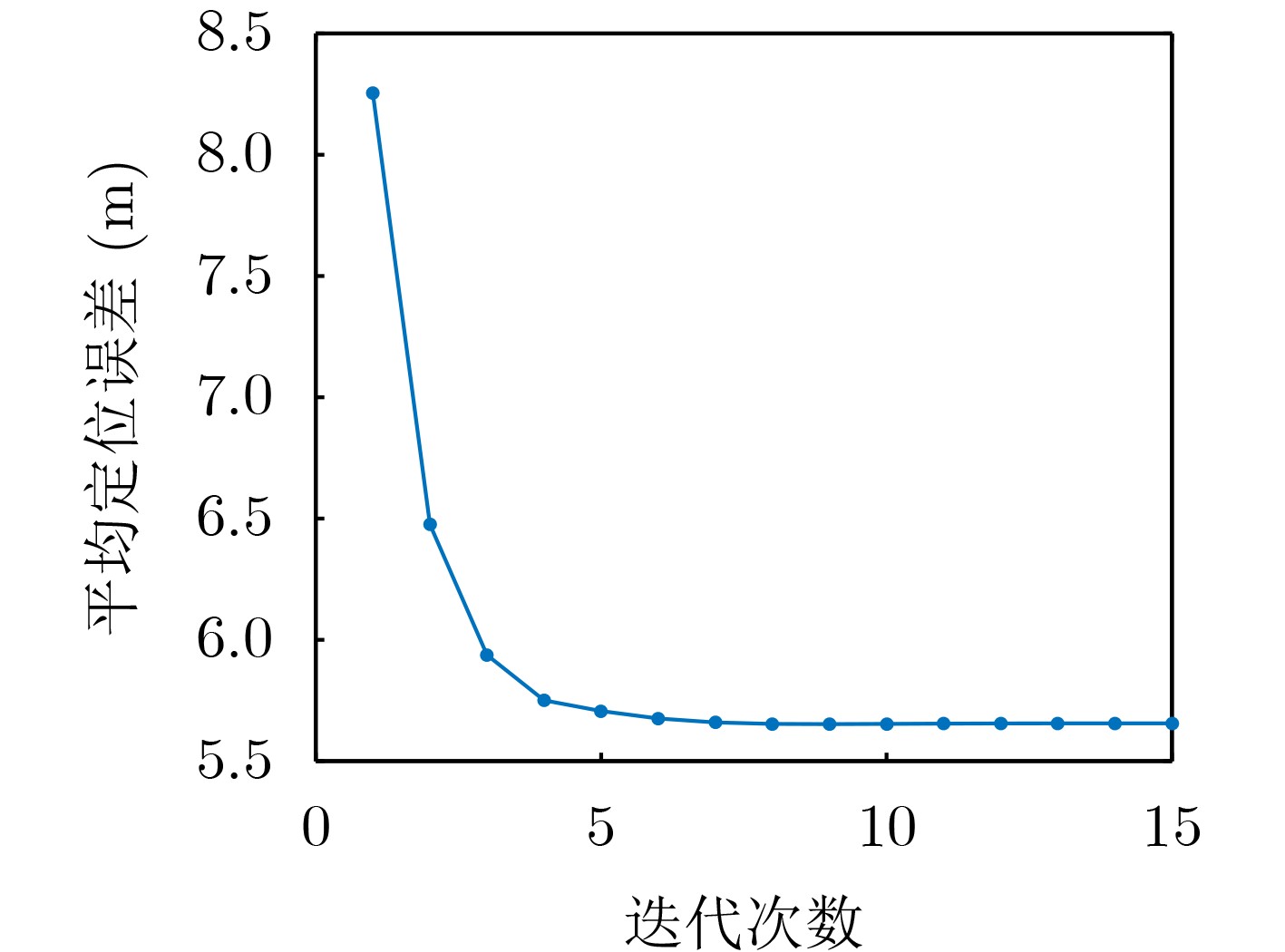
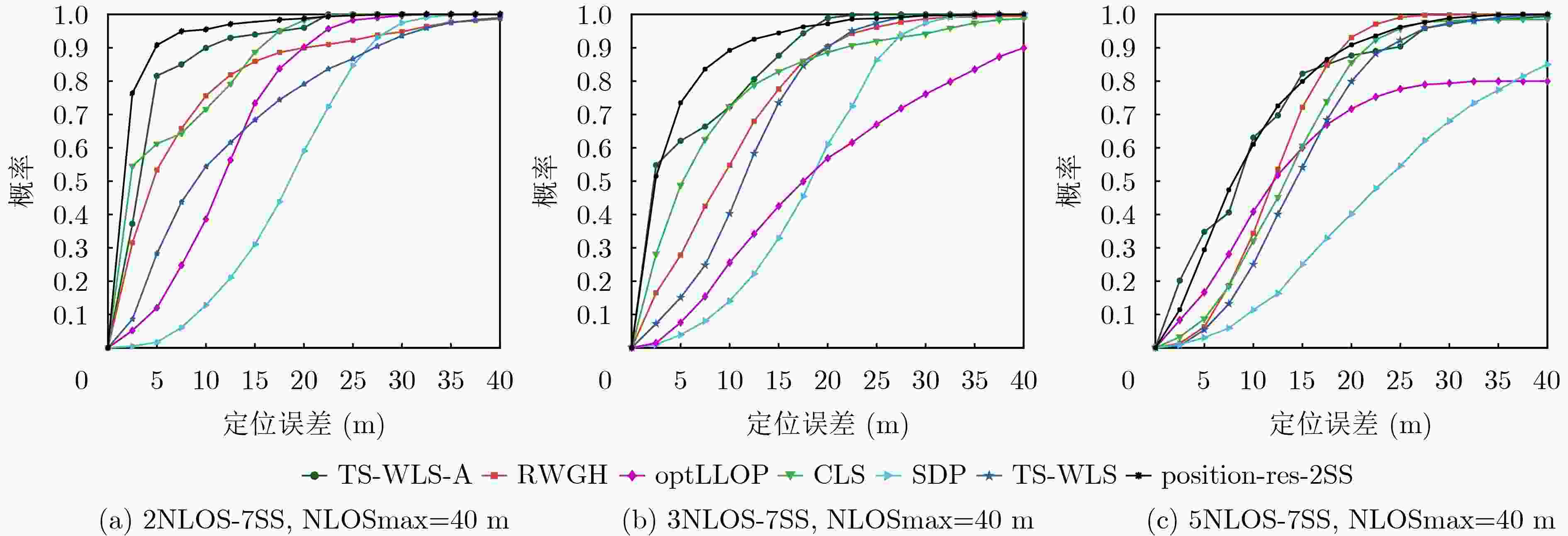
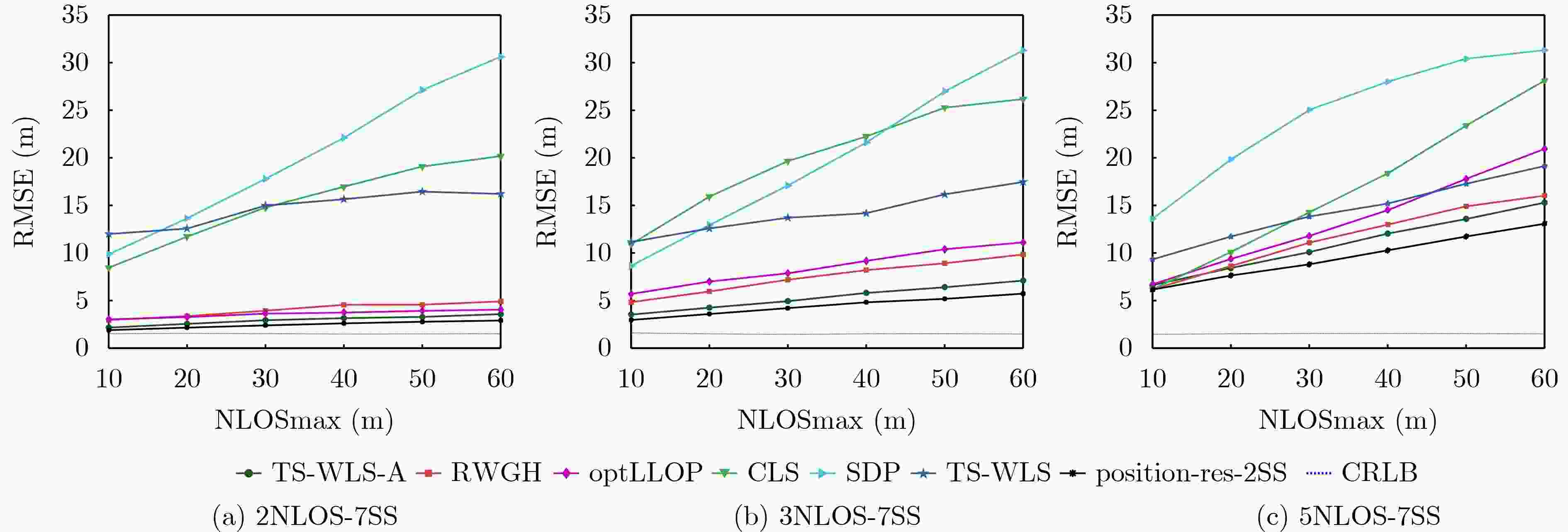
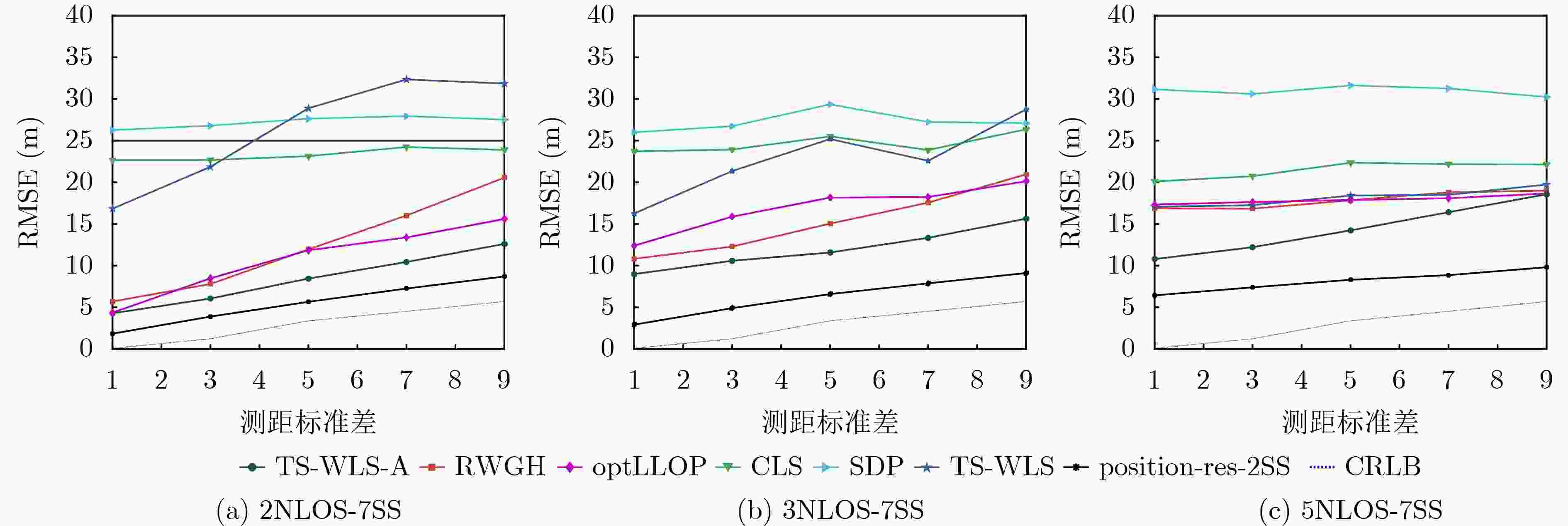
Abstract: Objective Wireless positioning technology has gained increasing attention in the Internet of Things (IoT), Intelligent Transportation Systems (ITS), and Location-Based Services (LBS). However, Non-Line-of-Sight (NLOS) errors remain a major obstacle to positioning accuracy. When Line-of-Sight (LOS) propagation between mobile and static sensors is blocked by obstacles, ranging measurement errors increase substantially. Suppressing or mitigating NLOS errors is therefore essential for improving wireless positioning performance. Although existing approaches—such as Kalman filtering, hybrid Time Difference of Arrival (TDOA)/Angle of Arrival (AOA) algorithms, and reinforcement learning—have shown some effectiveness, each faces limitations. Algorithm performance can be affected by network topology, lack adaptability in complex environments, or require high computational costs. Moreover, the statistical behavior of NLOS errors remains poorly characterized, making accurate positioning difficult in large-scale settings. This study proposes an Iterative Weighted Least Squares (IWLS) algorithm based on Time of Arrival (TOA) measurements. By defining position residuals and incorporating a residual-based weighting strategy into the WLS framework, the method suppresses NLOS errors effectively. Compared with traditional approaches, the proposed algorithm achieves higher positioning accuracy and better adaptability in NLOS scenarios, while retaining the ease of implementation offered by TOA-based techniques. Methods This study defines a new position residual based on TOA measurements from two Mobile Sensors (MSs). The residual typically approaches zero under LOS conditions but tends to increase significantly under NLOS conditions. As this residual effectively reflects deviations induced by NLOS errors, it is used to assign weights to individual equations within the linear positioning system. A residual-based weighting strategy is proposed, in which each weight is computed from the corresponding position residual, and the Weighted Least Squares (WLS) method is applied to regulate the influence of each equation. The position is estimated by iteratively updating the residuals, computing the associated weights, and applying WLS, thereby progressively reducing the positioning error and yielding an accurate estimate of the MS location. Results and Discussions The performance of the proposed algorithm is evaluated through computer simulations under varying Signal-to-Diffraction Ratio (SDR) and maximum NLOS error (NLOSmax) conditions. The simulation results indicate the following: (1) When the number of NLOS-affected static nodes is two, the Cumulative Distribution Function (CDF) of positioning error for the proposed IWLS algorithm is below 92%@5m, outperforming other tested algorithms and maintaining a consistent advantage (Fig. 6). (2) In the NLOSmax scenario (Fig. 7), the IWLS algorithm achieves better positioning accuracy than conventional methods when the number of NLOS-affected nodes is small. As this number increases, the error of the proposed algorithm grows more gradually. (3) In the SDR scenario (Fig. 8), although all algorithms show degraded performance as SDR increases, the IWLS algorithm consistently yields the lowest Root Mean Square Error (RMSE) and remains closest to the Cramér-Rao Lower Bound (CRLB). Conclusions This study proposes an IWLS localization algorithm inspired by the relationship between position residuals and the reliability of localization equations. A position residual is defined using range measurements from two static sensors, and a residual-based weighting strategy is developed to suppress the influence of NLOS errors. During each iteration, the weighting vector downregulates the contribution of equations affected by large NLOS errors, thereby improving positioning accuracy. Simulation results show that the IWLS algorithm outperforms conventional localization methods under NLOS conditions and achieves RMSE values close to the CRLB. Notably, when two static sensors are affected by NLOS errors, the localization RMSE can be reduced to approximately 2 m, representing 2% of the coverage radius.
- Wireless localization /
- Weighted Least Squares (WLS) /
- Time of Arrival (TOA) /
- Position residual /
- Non-Line-of-Sight (NLOS) error

HTML全文

图 1 位置残差示意图

下载: 全尺寸图片幻灯片

图 2 IWLS算法流程图

下载: 全尺寸图片幻灯片

图 3 不同权值计算方法的定位CDF性能

下载: 全尺寸图片幻灯片

图 4 不同权值计算方法的定位RMSE性能

下载: 全尺寸图片幻灯片

图 5 位置残差均值与迭代次数关系

下载: 全尺寸图片幻灯片

图 6 CDF性能比较：测距噪声标准差1 m

下载: 全尺寸图片幻灯片

图 7 RMSE性能比较：测距标准差1 m

下载: 全尺寸图片幻灯片

图 8 不同测距标准差的RMSE比较：NLOSmax=40 m

下载: 全尺寸图片幻灯片

表 1 对比方法描述

对比方法	描述
chan	YT Chan提出的TS-WLS定位算法^[25]
$2{\text{SS-R}}$	本文提出的位置残差倒数的1次幂
$2{\text{SS-}} {{\mathrm{R}}^2}$	本文提出的位置残差倒数的2次幂
$2{\text{SS-}}{{\mathrm{R}}^3}$	本文提出的位置残差倒数的3次幂

下载: 导出CSV

表 2 算法对比

算法	描述
CLS	约束最小二乘法^[22]
SDP	半正定规划算法^[23]
RWGH	残差加权算法^[24]
TS-WLS	已知TDOA测量值情况下，使用两步WLS算法^[26]
OptLLOP	扩展的LLOP算法^[27]
TS-WLS-A	基于角度残差的两步WLS算法^[28]
CRLB	克拉默-拉奥下界(Cramer-Rao Lower Bound)
position res-2SS	本文提出的以位置残差倒数为权值的IWLS算法

下载: 导出CSV

参考文献(29)

[1]	SAFA A and AL-ZAWQARI A. Co-design of a robot controller board and indoor positioning system for IoT-enabled applications[C]. 2024 International Conference on Microelectronics (ICM), Doha, Qatar, 2024: 1–6. doi: 10.1109/ICM63406.2024.10815886.
[2]	钱志鸿, 田春生, 郭银景, 等. 智能网联交通系统的关键技术与发展[J]. 电子与信息学报, 2020, 42(1): 2–19. doi: 10.11999/JEIT190787. QIAN Zhihong, TIAN Chunsheng, GUO Yinjing, et al. The key technology and development of intelligent and connected transportation system[J]. Journal of Electronics & Information Technology, 2020, 42(1): 2–19. doi: 10.11999/JEIT190787.
[3]	ABBA A M, SANUSI J, OSHIGA O, et al. A review of localization techniques in wireless sensor networks[C]. 2023 2nd International Conference on Multidisciplinary Engineering and Applied Science (ICMEAS), Abuja, Nigeria, 2023: 1–5. doi: 10.1109/ICMEAS58693.2023.10429886.
[4]	CHAMBON A, RACHEDI A, SAHLI A, et al. Managing a resilient multitier architecture for unstable IoT networks in location based-services[J]. IEEE Transactions on Network and Service Management, 2024, 21(5): 5304–5320. doi: 10.1109/TNSM.2024.3449044.
[5]	CUI Jianfeng, LIANG Hong, WANG Zhiwen, et al. Spatial distribution characteristics of positioning accuracy for TOA localization[J]. IEEE Sensors Journal, 2025, 25(3): 5003–5012. doi: 10.1109/JSEN.2024.3512613.
[6]	LIN Yupei, LI Yicheng, SONG Dan, et al. Sensor selection for TOA-based multitarget localization with nonshared sensors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2025, 61(2): 2383–2396. doi: 10.1109/TAES.2024.3469919.
[7]	HUANG Lixiong, CHEN Ruizhi, CHEN Ying, et al. Robust TDOA-based indoor localization using improved clock-sync-scheme and multilevel constrained ARPF[J]. IEEE Sensors Journal, 2023, 23(10): 10633–10643. doi: 10.1109/JSEN.2023.3259540.
[8]	ZOU Yanbin. Semidefinite programming algorithms for 3-D AOA-based hybrid localization[J]. IEEE Open Journal of Signal Processing, 2023, 4: 294–303. doi: 10.1109/OJSP.2023.3279010.
[9]	左燕, 陈志猛, 蔡立平. 基于约束总体最小二乘的单站DOA/TDOA联合误差校正与定位算法[J]. 电子与信息学报, 2019, 41(6): 1317–1323. doi: 10.11999/JEIT180655. ZUO Yan, CHEN Zhimeng, and CAI Liping. Single-observer DOA/TDOA registration and passive localization based on constrained total least squares[J]. Journal of Electronics & Information Technology, 2019, 41(6): 1317–1323. doi: 10.11999/JEIT180655.
[10]	秦耀璐, 杨淑萍, 束锋, 等. 基于TDOA/FDOA多星联合定位误差与卫星构型分析[J]. 电波科学学报, 2018, 33(5): 565–574. doi: 10.13443/j.cjors.2017080903. QIN Yaolu, YANG Shuping, SHU Feng, et al. TDOA/FDOA joint location errors and satellite configuration for passive multi-satellite localization systems[J]. Chinese Journal of Radio Science, 2018, 33(5): 565–574. doi: 10.13443/j.cjors.2017080903.
[11]	孙霆, 董春曦, 毛昱. 一种基于半定松弛技术的TDOA-FDOA无源定位算法[J]. 电子与信息学报, 2020, 42(7): 1599–1605. doi: 10.11999/JEIT190435. SUN Ting, DONG Chunxi, and MAO Yu. A TDOA-FDOA passive positioning algorithm based on the semi-definite relaxation technique[J]. Journal of Electronics & Information Technology, 2020, 42(7): 1599–1605. doi: 10.11999/JEIT190435.
[12]	束锋, 朱伟强, 陆锦辉, 等. 基于最大比合并的最大似然TDOA/FDOA联合定位方法[J]. 宇航学报, 2010, 31(4): 1143–1148. doi: 10.3873/j.issn.1000-1328.2010.04.033. SHU Feng, ZHU Weiqiang, LU Jinhui, et al. Maximum ratio combining based maximum likelihood TDOA/FDOA joint localization[J]. Journal of Astronautics, 2010, 31(4): 1143–1148. doi: 10.3873/j.issn.1000-1328.2010.04.033.
[13]	BAI Jiatong, CHEN Minghao, LI Yifan, et al. Multi-modal iterative and deep fusion frameworks for enhanced passive DOA sensing via a green massive H2AD MIMO receiver[J]. IEEE Transactions on Green Communications and Networking, 2025. doi: 10.1109/TGCN.2025.3543476.
[14]	WANG Fang, TANG Hai, and CHEN Jialei. Survey on NLOS identification and error mitigation for UWB indoor positioning[J]. Electronics, 2023, 12(7): 1678. doi: 10.3390/electronics12071678.
[15]	QIN Zhengyang, MENG Zhaozong, LI Zhen, et al. Compensating the NLoS occlusion errors of UWB for pedestrian localization with MIMU[J]. IEEE Sensors Journal, 2023, 23(11): 12146–12158. doi: 10.1109/JSEN.2023.3266433.
[16]	CHEN Haishao, CAO Li; and YUE Yinggao. TDOA/AOA hybrid localization based on improved dandelion optimization algorithm for mobile location estimation under NLOS simulation environment[J]. Wireless Personal Communications, 2023, 131(4): 2747–2772. doi: 10.1007/s11277-023-10578-y.
[17]	BIANCHI V, CIAMPOLINI P, and DE MUNARI I. RSSI-based indoor localization and identification for ZigBee wireless sensor networks in smart homes[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68(2): 566–575. doi: 10.1109/TIM.2018.2851675.
[18]	ALAGHA A, SINGH S, MIZOUNI R, et al. Target localization using multi-agent deep reinforcement learning with proximal policy optimization[J]. Future Generation Computer Systems, 2022, 136: 342–357. doi: 10.1016/j.future.2022.06.015.
[19]	闻建刚, 岳洋洋, 华惊宇, 等. NLOS状态信息辅助协方差矩阵修正的无线网络定位方法[J]. 传感技术学报, 2022, 35(11): 1561–1567. doi: 10.3969/j.issn.1004-1699.2022.011.017. WEN Jiangang, YUE Yangyang, HUA Jingyu, et al. Wireless network positioning method with covariance matrix correction assisted by NLOS state information[J]. Chinese Journal of Sensors and Actuators, 2022, 35(11): 1561–1567. doi: 10.3969/j.issn.1004-1699.2022.011.017.
[20]	尹烨佳, 华惊宇, 李枫, 等. 非视距环境中的无线网络残差加权定位算法[J]. 传感技术学报, 2019, 32(5): 749–755. doi: 10.3969/j.issn.1004-1699.2019.05.019. YIN Yejia, HUA Jingyu, LI Feng, et al. Residual weighted based wireless localization algorithm in NLOS environments[J]. Chinese Journal of Sensors and Actuators, 2019, 32(5): 749–755. doi: 10.3969/j.issn.1004-1699.2019.05.019.
[21]	HUA Jingyu, YIN Yejia, WANG Anding, et al. Geometry-based non-line-of-sight error mitigation and localization in wireless communications[J]. Science China Information Sciences, 2019, 62(10): 202301. doi: 10.1007/s11432-019-9909-5.
[22]	KE Wei and WU Lenan. Constrained least squares algorithm for TOA-based mobile location under NLOS environments[C]. 2009 5th International Conference on Wireless Communications, Networking and Mobile Computing, Beijing, China, 2009: 1–4. doi: 10.1109/WICOM.2009.5302854.
[23]	GHARI P M, SHAHBAZIAN R, and GHORASHI S A. Wireless sensor network localization in harsh environments using SDP relaxation[J]. IEEE Communications Letters, 2016, 20(1): 137–140. doi: 10.1109/LCOMM.2015.2498179.
[24]	CHEN Pichun. A non-line-of-sight error mitigation algorithm in location estimation[C]. 1999 IEEE Wireless Communications and Networking Conference, New Orleans, USA, 1999: 316–320. doi: 10.1109/WCNC.1999.797838.
[25]	CHAN Y T and HO K C. A simple and efficient estimator for hyperbolic location[J]. IEEE Transactions on Signal Processing, 1994, 42(8): 1905–1915. doi: 10.1109/78.301830.
[26]	BISWAS P and YE Yinyu. Semidefinite programming for ad hoc wireless sensor network localization[C]. The 3rd International Symposium on Information Processing in Sensor Networks, Berkeley, USA, 2004: 46–54. doi: 10.1145/984622.984630.
[27]	ZHENG Xiaoneng, HUA Jingyu, ZHENG Zhilong, et al. LLOP localization algorithm with optimal scaling in NLOS wireless propagations[C]. 2013 IEEE 4th International Conference on Electronics Information and Emergency Communication, Beijing, China, 2013: 45–48. doi: 10.1109/ICEIEC.2013.6835450.
[28]	WANG Jiale, WEN Jiangang, HUA Jingyu, et al. Angle residual-based NLOS suppression and localization method in wireless sensor networks[J]. IEEE Sensors Journal, 2023, 23(13): 14388–14396. doi: 10.1109/JSEN.2023.3275627.
[29]	CHAN Y T, TSUI W Y, SO H C, et al. Time-of-arrival based localization under NLOS conditions[J]. IEEE Transactions on Vehicular Technology, 2006, 55(1): 17–24. doi: 10.1109/TVT.2005.861207.