Dirichlet过程混合模型驱动的多站时差信号分选方法

陈金立; 王延杰; 樊宇; 李家强

doi:10.11999/JEIT250191

Dirichlet过程混合模型驱动的多站时差信号分选方法

doi: 10.11999/JEIT250191 cstr: 32379.14.JEIT250191

南京信息工程大学电子与信息工程学院南京 210044

基金项目: 国家自然科学基金(62071238)，江苏省自然科学基金(BK20191399)，江苏省研究生科研与实践创新计划项目(KYCX25_1645)

详细信息

作者简介:
陈金立：男，教授，研究方向为雷达辐射源信号分选、MIMO雷达信号处理

王延杰：男，硕士生，研究方向为电子侦察与雷达信号分选

樊宇：男，硕士生，研究方向为辐射源特征提取与识别

李家强：男，副教授，研究方向为雷达信号处理

通讯作者:
陈金立　chen820803@yeah.net

中图分类号: TN971
计量
- 文章访问数: 63
- HTML全文浏览量: 31
- PDF下载量: 5
- 被引次数: 0
出版历程
- 收稿日期: 2025-03-24
- 修回日期: 2025-08-29
- 网络出版日期: 2025-09-09

Signal Sorting Method Based on Multi-station Time Difference and Dirichlet Process Mixture Model

School of Electronic and Information Engineering, Nanjing University of Information Science and Technology, Nanjing 210044, China

Funds: The National Natural Science Foundation of China (62071238), The National Nature Science Foundation of Jiangsu Province (BK20191399), The Postgraduate Research & Practice Innovation Program of Jiangsu Province (KYCX25_1645)

摘要

摘要: 现有的多站时差信号分选方法依赖辐射源数目或脉冲参数测量误差等先验信息，并且无法对配对失败的脉冲进行准确分选。针对这一问题，该文提出一种Dirichlet过程混合模型(DPMM)驱动的多站时差分选方法。该方法首先引入时差窗与多参数约束条件，实现大部分脉冲的成功配对，同时部分脉冲会由于脉冲丢失与噪声干扰而配对失败；接着，采用DPMM对配对成功后获得的到达时差信息进行聚类分析，从而实现对配对成功脉冲的分选，并构建雷达脉冲集合；最后，通过计算配对失败脉冲相对于脉冲集合的归属度，完成对配对失败脉冲的归类。仿真结果表明，与现有方法相比，该方法无需事先确定辐射源数目或参数测量误差等参数，且在脉冲丢失和干扰严重的情况下，仍能保持较高的分选准确率。
- 信号分选 /
- 脉冲配对 /
- 到达时差 /
- Dirichlet过程混合模型
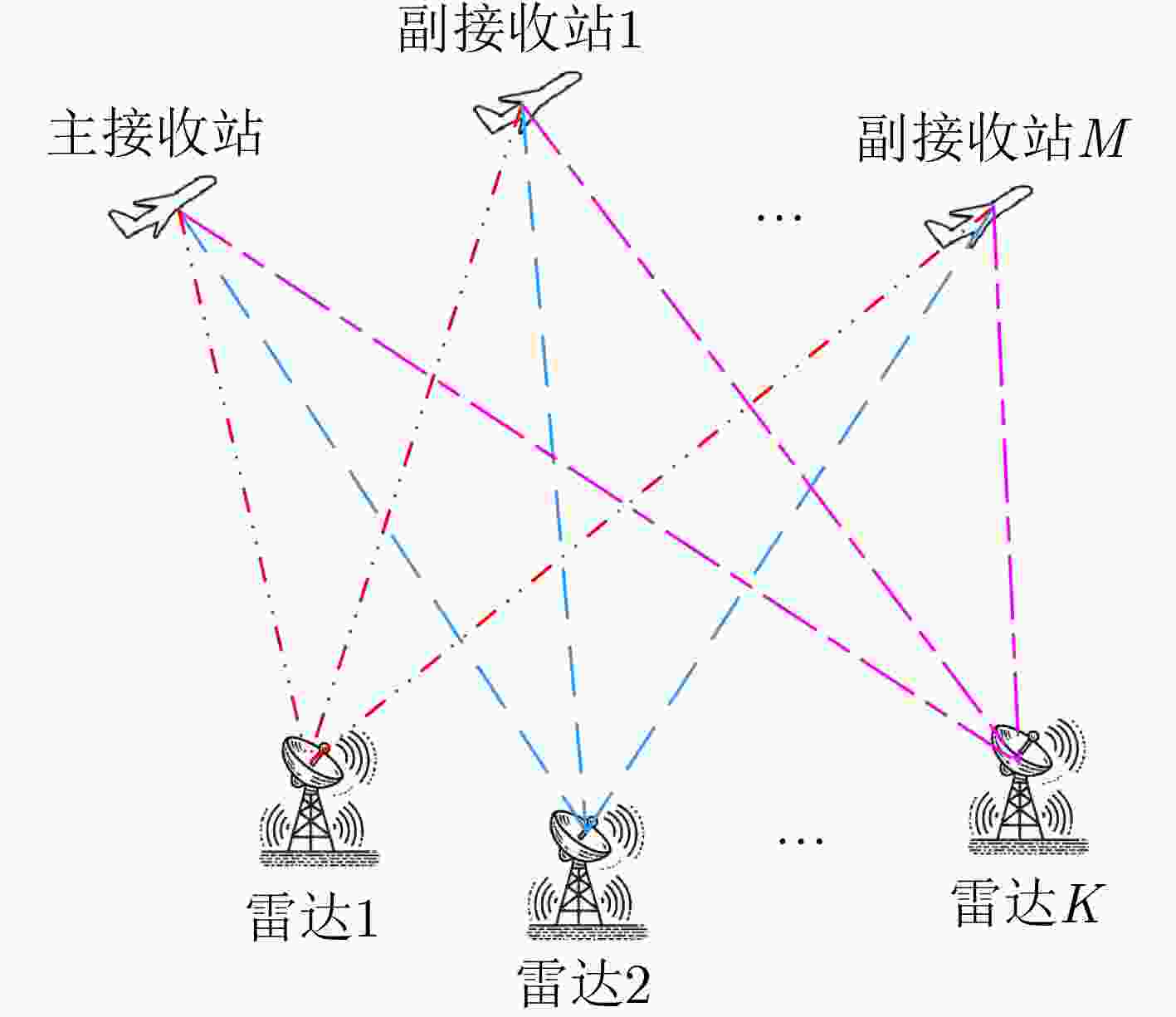
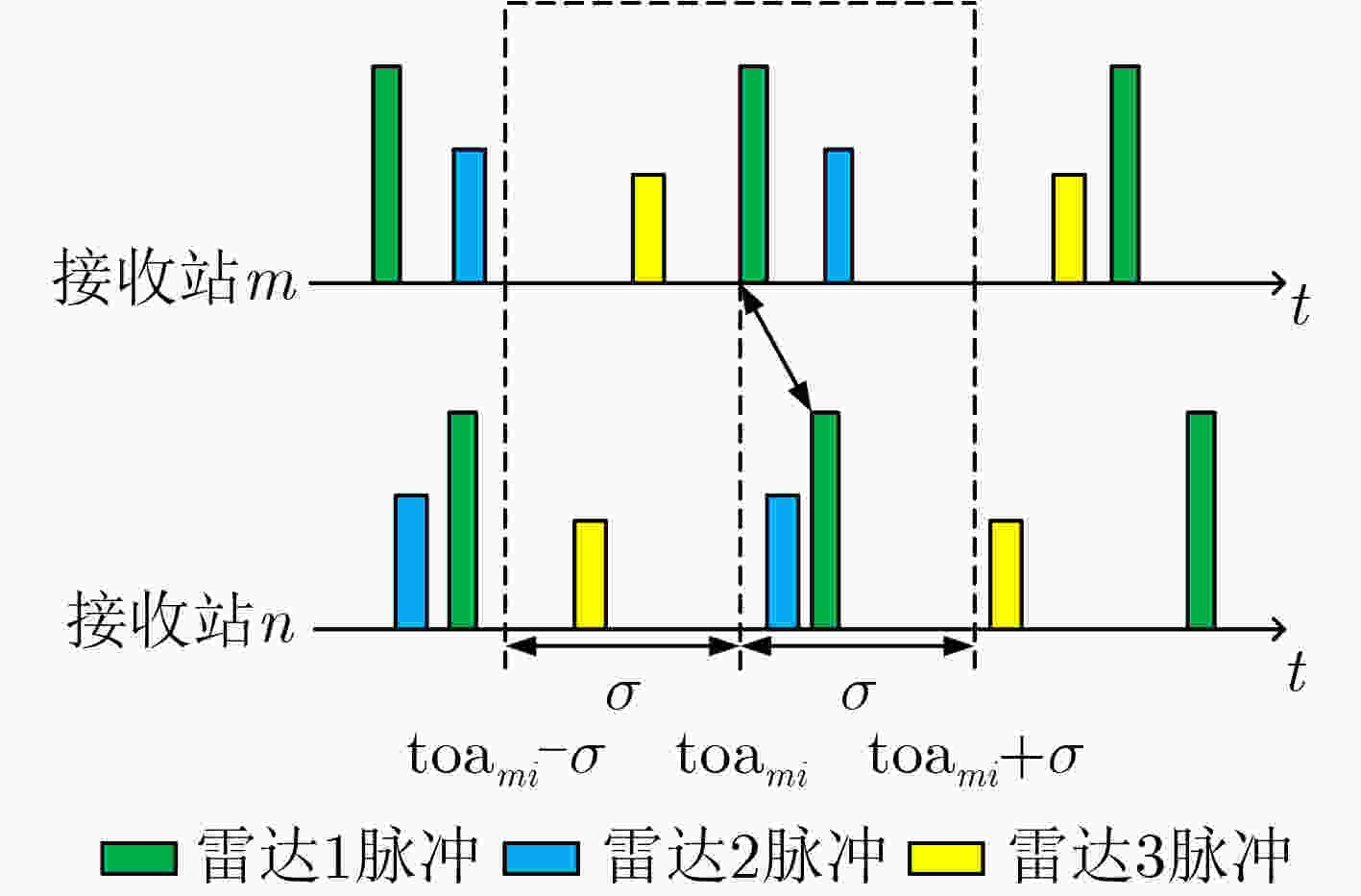
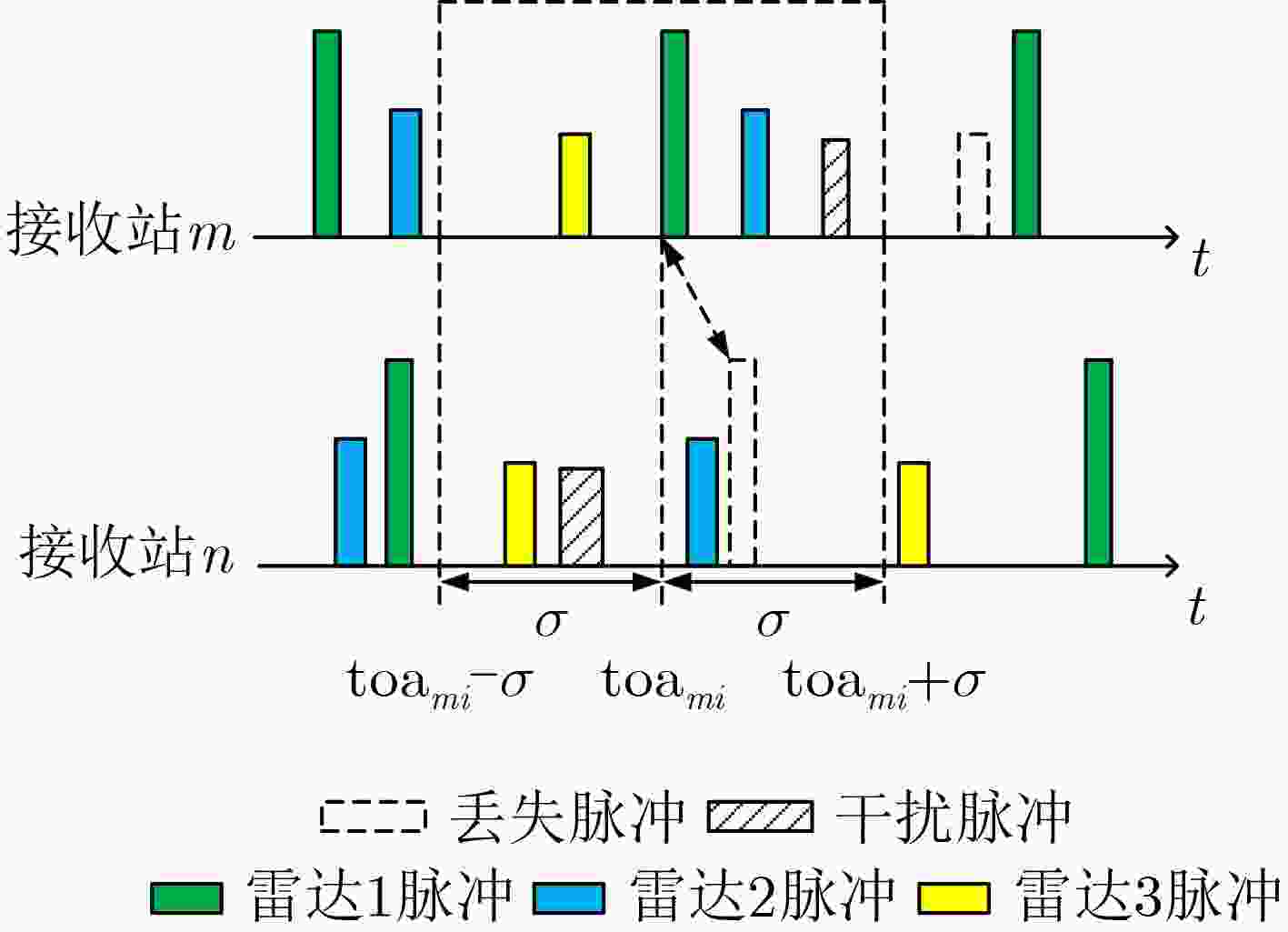
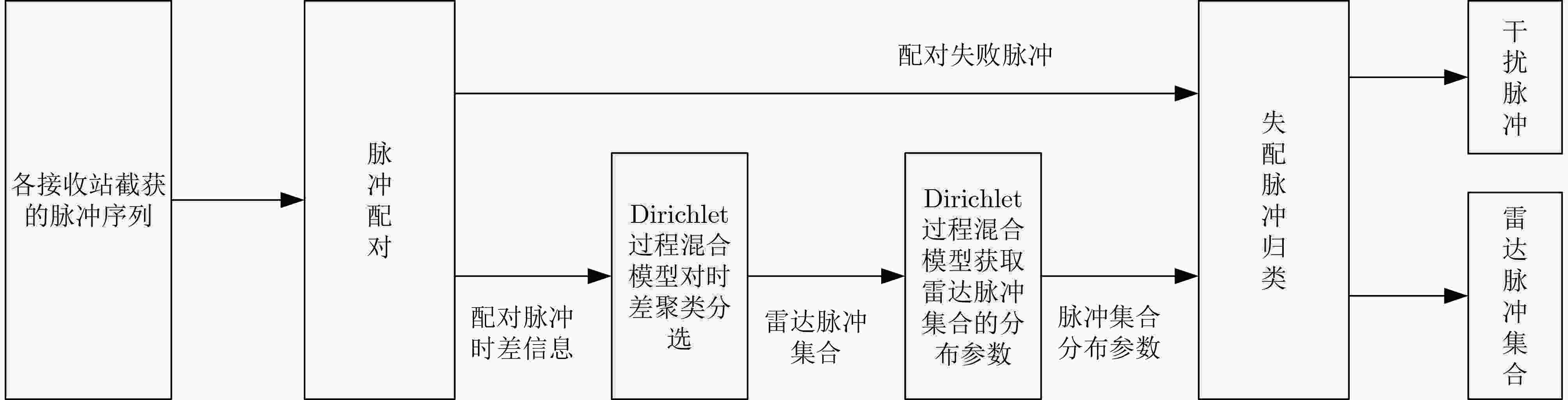
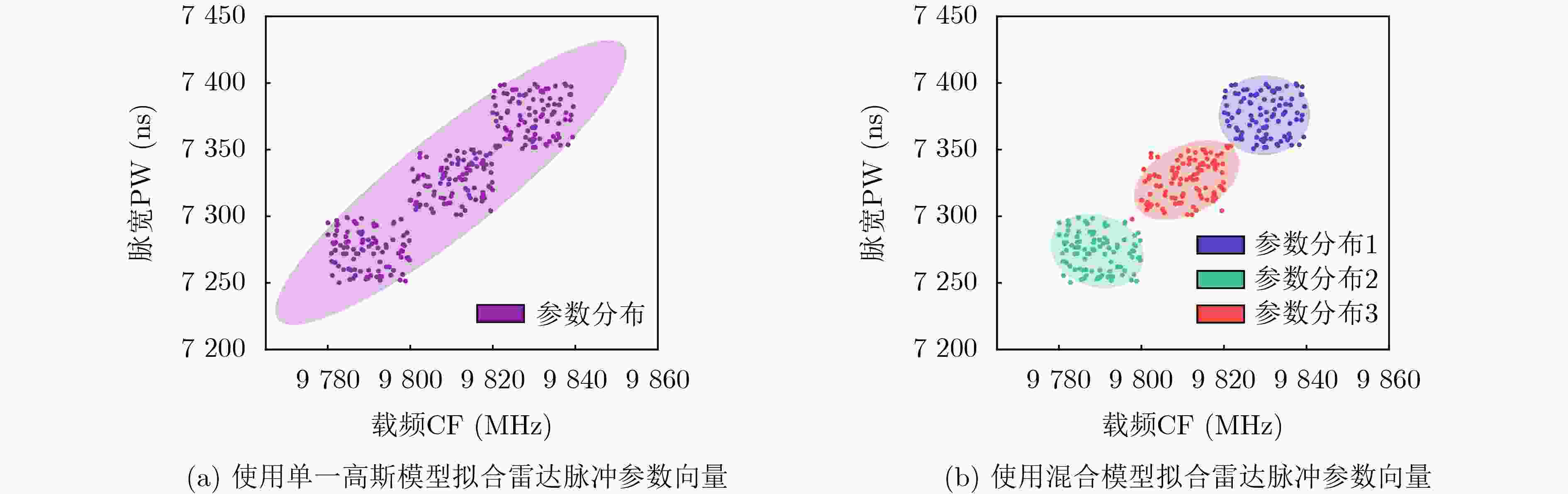
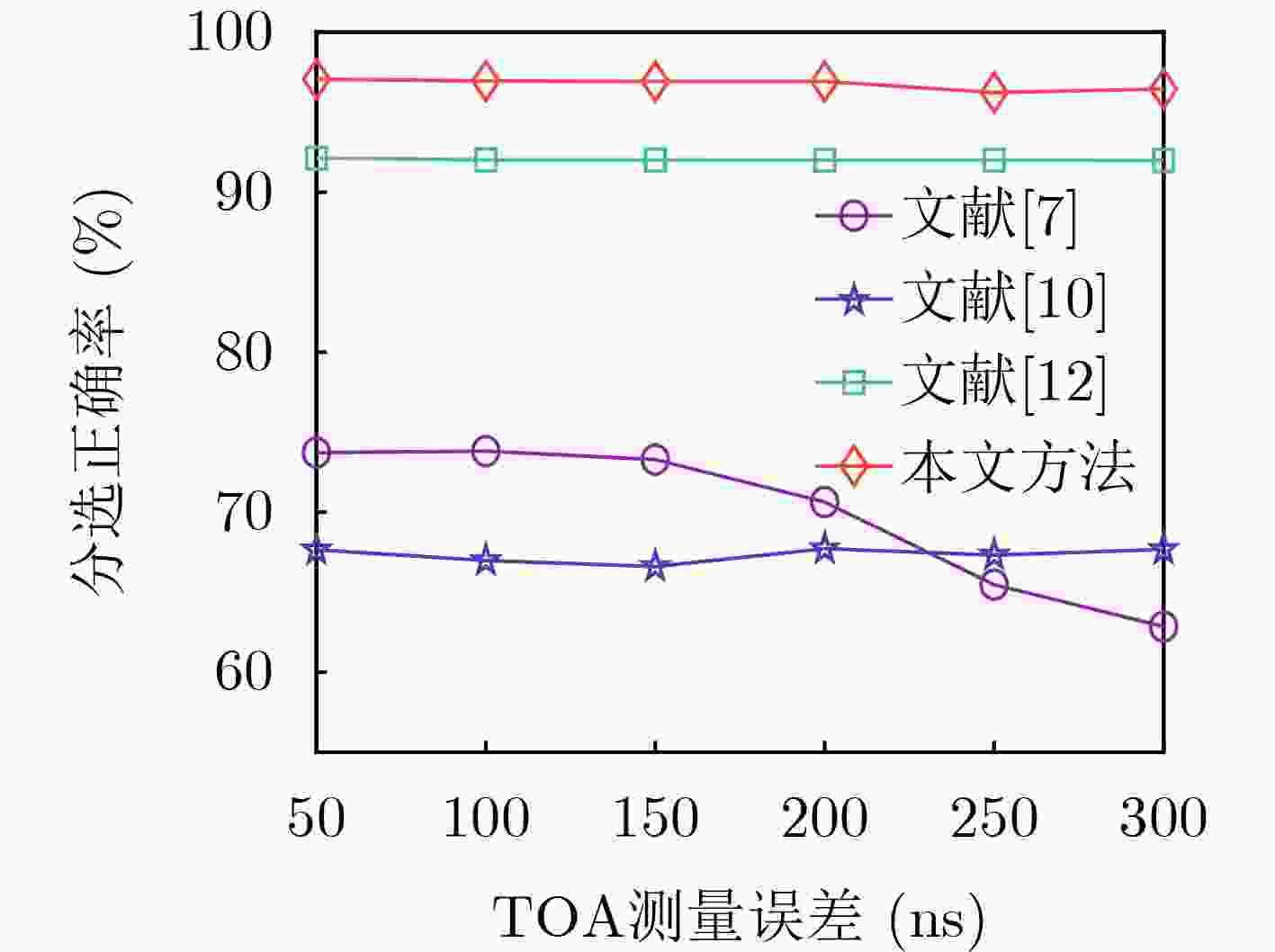
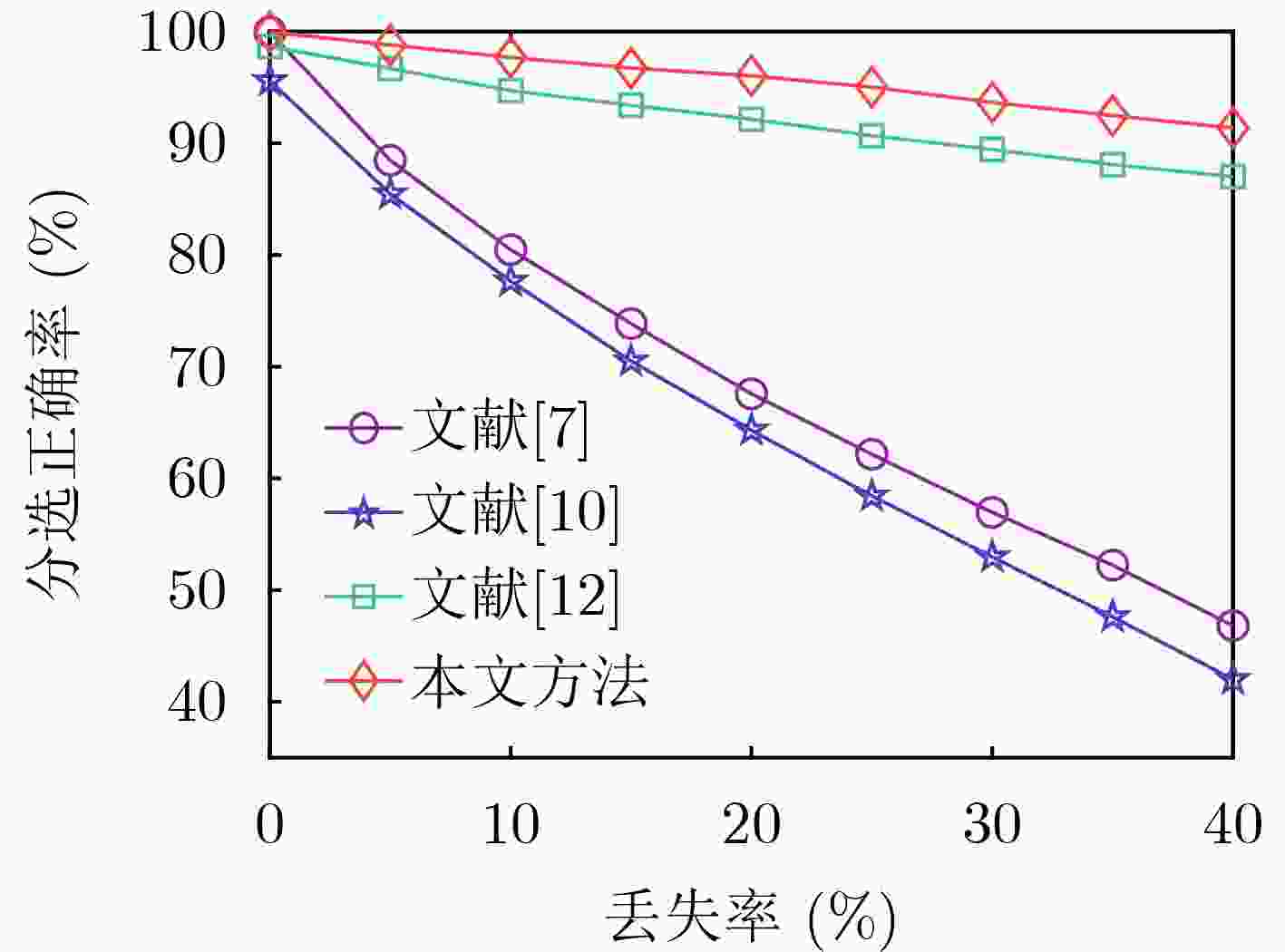
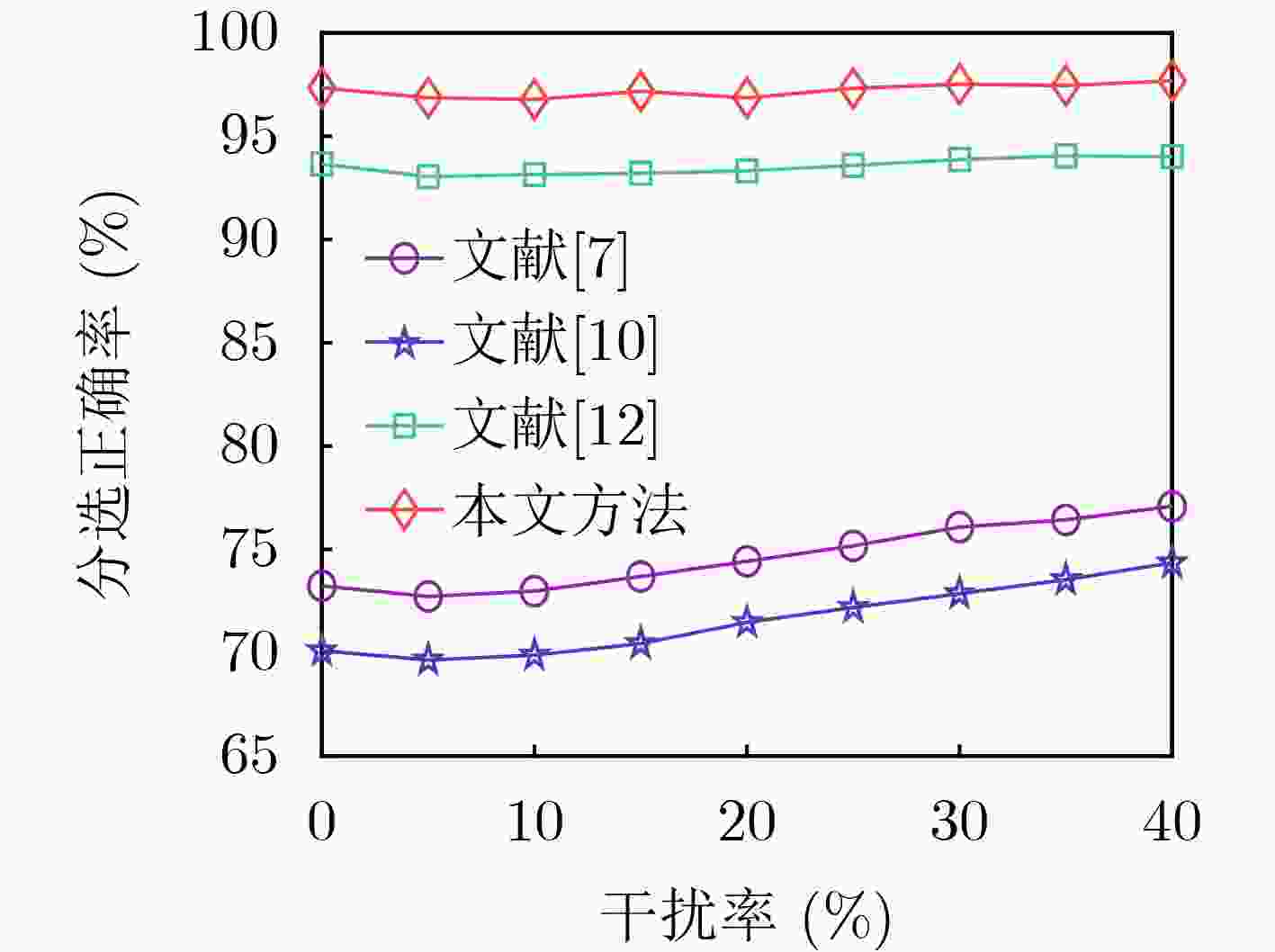
Abstract: Objective Signal sorting is a crucial technology in electronic reconnaissance that enables the deinterleaving of mixed pulse sequences emitted by multiple radar radiation sources, thereby supporting military decision-making. With the rapid advancement of electronic technology, multi-station cooperative signal sorting has received increasing attention. However, existing multi-station signal sorting methods depend heavily on manually selected parameters, which limits adaptability. Moreover, in complex environments with pulse loss and noise interference, conventional methods struggle to process unpaired pulses effectively, reducing the accuracy and stability of sorting. To address these challenges, this study applies the Dirichlet Process Mixture Model (DPMM) to multi-station cooperative signal sorting. The proposed approach enables adaptive sorting even when the number of radiation sources is unknown or measurement errors exist, thereby improving flexibility and adaptability. Furthermore, it can effectively classify unpaired pulses caused by pulse loss or noise, enhancing the robustness and reliability of sorting. This research provides a novel strategy for signal sorting in complex electromagnetic environments and holds promising application value in radar signal processing. Methods In multi-station cooperative signal sorting, the spatial distribution of multiple receiving stations detecting the same radar signal makes efficient and accurate signal pairing and classification a core challenge. To address this issue, a multi-station cooperative signal sorting method based on the DPMM is proposed. The process comprises three stages: pulse pairing, time-difference clustering and sorting, and mismatched pulse classification. In the pulse pairing stage, identical pulses originating from the same radiation source are identified from the sequences intercepted by each receiving station. To ensure accurate pairing, a dual-constraint strategy is adopted, combining a time-difference window with multi-parameter matching. Successfully paired pulses are then constructed into a time-difference vector set, which provides the data foundation for the subsequent clustering and sorting stage. In the time-difference clustering and sorting stage, DPMM is employed to cluster the time-difference vector set. DPMM adaptively determines the number of clusters to model the data structure, enabling the system to infer the optimal cluster count. Gibbs sampling is used to optimize model parameters, further enhancing clustering robustness. Based on the clustering results, radar pulse sets are constructed, achieving signal sorting across multiple radiation sources. In the mismatched pulse classification stage, unpaired pulses caused by noise interference or pulse loss during transmission are further processed. DPMM is applied to fit radar pulse parameter vectors, including pulse width, radio frequency, and bandwidth. The affiliation degree of each mismatched pulse relative to the radar pulse sets is then calculated. Pulses with affiliation degrees exceeding a predefined threshold are merged into the corresponding pulse set, whereas those below the threshold are classified as anomalous pulses, likely due to interference or noise, and are discarded. This method enhances the adaptability and robustness of multi-station cooperative signal sorting and provides an effective solution for complex electromagnetic environments. Results and Discussions In the experimental validation, radar pulse data are generated through simulation to evaluate the effectiveness of the proposed method. Compared with traditional multi-station cooperative signal sorting approaches, the method achieves high-precision sorting without requiring prior knowledge of the number of radiation sources or parameter measurement errors, thereby demonstrating strong adaptability and practicality. To comprehensively assess performance in complex environments, simulations are conducted to analyze sorting capability under varying measurement errors, pulse loss rates, and interference rates. The final sorting results are summarized in (Table. 3). The results indicate that even in the presence of noise interference and data loss, most radar pulses are accurately identified, with only a small fraction misclassified as interference signals. The final sorting accuracy reaches 98.8%, confirming the robustness and stability of the method against pulse loss, noise, and other uncertainties. To further validate its superiority, the method is compared with other algorithms under different conditions. Sorting accuracy under different Time of Arrival (TOA) measurement errors (Fig. 6) shows that stable performance is maintained even under severe noise interference, reflecting strong noise resistance. Further analyses of sorting accuracy under different pulse loss rates and interference rates (Figs. 7 and 8) demonstrate that higher efficiency and stability are achieved in handling unpaired pulses, and pulses that fail to be paired are more accurately classified. The sorting accuracy of different algorithms in various scenarios (Fig. 9) further confirms that the method performs more consistently in complex environments, indicating higher adaptability. Overall, the method adapts well to diverse application scenarios and provides efficient, stable, and reliable signal sorting for multi-station cooperative electronic reconnaissance tasks. Conclusions This study proposes a multi-station cooperative signal sorting method based on the DPMM to address the limitations of traditional approaches, which rely heavily on prior information and perform poorly in processing unpaired pulses. By applying DPMM for adaptive clustering of time-difference information, the proposed method avoids sorting errors caused by improper manual parameter settings and effectively classifies unpaired pulses based on radar pulse parameter characteristics. Simulation results show that this method not only improves the accuracy and stability of multi-station cooperative signal sorting but also maintains high sorting performance even when the number of radiation sources is unknown or measurement errors are present, highlighting its engineering application value. Future research may extend this approach to dynamic electromagnetic environments and adaptive real-time processing to meet the demands of more complex electronic reconnaissance tasks.
- Signal sorting /
- Pulse pairing /
- Time Difference Of Arrival (TDOA) /
- Dirichlet Process Mixture Model (DPMM)

HTML全文

图 1 多站协同侦察场景图

下载: 全尺寸图片幻灯片

图 2 脉冲时差窗配对原理图

下载: 全尺寸图片幻灯片

图 3 实际混合脉冲序列图

下载: 全尺寸图片幻灯片

图 4 基于Dirichlet过程混合模型的多站时差分选方法框图

下载: 全尺寸图片幻灯片

图 5 单一模型与混合模型拟合效果对比图

下载: 全尺寸图片幻灯片

图 6 分选正确率随TOA测量误差的变化曲线

下载: 全尺寸图片幻灯片

图 7 分选正确率随丢失率的变化曲线

下载: 全尺寸图片幻灯片

图 8 分选正确率随干扰率的变化曲线

下载: 全尺寸图片幻灯片

图 9 不同场景下各算法分选正确率比较

下载: 全尺寸图片幻灯片

表 1 场景1中雷达参数表

雷达序号	位置坐标(km)	PRI(μs)	PW(μs)	CF(MHz)	BW(MHz)	发射脉冲数
E1	($ - $6.0, 0)	350抖动	11固定	2 500固定	7.8/7.9跳变	185
E2	($ - $4.7, 1.7)	420/610参差	10/10.5跳变	2 400固定	7固定	164
E3	($ - $3.8, 3.2)	550固定	10.3固定	2 200/2 600跳变	6/8跳变	100
E4	($ - $2.5, 4.3)	1 240～1 300滑变	12.3固定	1 800固定	7.8/6.5跳变	90
E5	($ - $0.9, 5.5)	1 630固定	10固定	2 450～2 550滑变	8.5固定	74
E6	(1.8, 4.5)	2 000/2 250/2 500参差	7.8/8/9.2跳变	2 800固定	5固定	61
E7	(2.5, $ - $4.0)	5 000抖动	9.7固定	600/750跳变	4.9/5.6跳变	56
E8	(4.6, $ - $1.8)	7 000抖动	9固定	1 500固定	3.2固定	42
E9	(6.0, 0)	10 000固定	7.5固定	2 100～2 200滑变	5.4固定	30
总数						802

下载: 导出CSV

表 2 接收站实际接收脉冲数

雷达序号	接收站1	接收站2	接收站3
E1	168	160	141
E2	149	138	136
E3	91	92	82
E4	83	78	78
E5	67	63	57
E6	56	53	52
E7	53	50	46
E8	40	35	40
E9	28	29	24
干扰脉冲	147	104	66
接收脉冲总数	882	802	722
配对成功脉冲	518	518	518

下载: 导出CSV

表 3 基于Dirichlet过程混合模型的多站时差分选结果

雷达序号	接收站1		接收站2		接收站3
雷达序号	正确分选脉冲	漏选脉冲	正确分选脉冲	漏选脉冲	正确分选脉冲	漏选脉冲
E1	166	2	158	2	141	0
E2	148	1	137	1	133	3
E3	91	0	90	2	82	0
E4	83	0	76	2	78	0
E5	65	2	60	3	56	1
E6	56	0	53	0	50	2
E7	51	2	49	1	45	1
E8	39	1	34	1	40	0
E9	27	1	28	1	24	0
干扰脉冲	156		117		73
分选正确率	98.8%

下载: 导出CSV

表 4 场景2中雷达参数表

雷达序号	位置坐标(km)	PRI(μs)	PW(μs)	CF(MHz)	BW(MHz)	发射脉冲数
E1	($ - $6.0, 0)	580固定	10.3固定	2 200～2 600滑变	6～8滑变	175
E2	($ - $4.8, 1.8)	400/600参差	10/10.5跳变	2 400～2 500滑变	8.5固定	156
E3	($ - $3.5, 3.5)	1 000～1 200滑变	10.1固定	2 250/2 500跳变	7/7.8跳变	103
E4	($ - $2.4, 4.5)	1 240～1 300滑变	9～9.5滑变	1 800固定	6.5/7.5跳变	94
E5	($ - $1.3, 5.5)	1 500固定	9.2固定	1 500～2 000滑变	7固定	75
E6	(3.5, $ - $4.5)	1 800/2 000/2 200参差	7.8/8/9.2跳变	700固定	4.8～5.4滑变	60
E7	(2.5, $ - $4.0)	3 000抖动	8.1固定	600/750跳变	4.5/5跳变	58
E8	(4.6, $ - $1.5)	5 000抖动	8～8.5滑变	2 150固定	4.5固定	42
E9	(0, $ - $6.0)	6 000固定	7.5固定	2 100～2 200滑变	5～5.6滑变	30
总数						793

下载: 导出CSV

表 5 场景3中雷达参数表

雷达序号	位置坐标(km)	模式	PRI(μs)	PW(μs)	CF(MHz)	BW(MHz)	发射脉冲数
E1	($ - $6.0, 0)	模式1	550固定	10固定	2 600～2 800滑变	8固定	216
E1	($ - $6.0, 0)	模式2	450/600参差	10/10.8跳变	2 800～3 000滑变	8.5固定	210
E2	($ - $4.0, 2.0)	模式1	1 000～1 200滑变	8.5～9滑变	2 400/2 600跳变	7.3/7.8跳变	180
E2	($ - $4.0, 2.0)	模式2	1 240～1 300滑变	9～9.5滑变	2 500固定	6.5固定	175
E3	($ - $3.8, $ - $3.2)	模式1	1 600固定	7.5～8.3滑变	1 100～1 300滑变	5.2/5.6跳变	160
E4	($ - $2.5, 4.3)	模式1	2 000/2 400参差	7.5固定	600固定	4.5～5滑变	155
		模式2	2 000固定	7～7.5滑变	750/900跳变	5固定	150
		模式3	2 400固定	8固定	1 000～1 200滑变	5.4固定	145
E5	(2.5, $ - $4.0)	模式1	2 800抖动	8.5固定	650/780跳变	4.8/5.5跳变	125
E6	(3.4, $ - $4.4)	模式1	2 600固定	9.3固定	1 600～1 800滑变	4固定	120
E6	(3.4, $ - $4.4)	模式2	2 500/2 700参差	9.8固定	1 700固定	4.5固定	110
E7	(2.7, $ - $4.0)	模式1	1 700～1 900滑变	12/12.5跳变	3 500/3 600跳变	10/10.5跳变	100
E7	(2.7, $ - $4.0)	模式2	1 900～2 100滑变	12.5固定	3 600固定	10.5固定	98
E8	(4.5, $ - $1.5)	模式1	2 500抖动	11.8固定	3 800～4 000滑变	10.8固定	70
E9	(6.0, $ - $6.0)	模式1	2 500～3 000滑变	11固定	2 600固定	8.5～9滑变	60
		模式2	3 000固定	11～11.5滑变	2 600/2 900跳变	9.0固定	68
		模式3	4 000固定	11.5固定	3 000～3 200滑变	9.5～10滑变	55
总数							2 197

下载: 导出CSV

参考文献(19)

[1]	XIANG Haoran, SHEN Furao, and ZHAO Jian. Deep TOA mask-based recursive radar pulse deinterleaving[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(2): 989–1006. doi: 10.1109/TAES.2022.3193948.
[2]	ZHOU Zixiang, FU Xiongjun, DONG Jian, et al. Radar signal sorting with multiple self-attention coupling mechanism based transformer network[J]. IEEE Signal Processing Letters, 2024, 31: 1765–1769. doi: 10.1109/LSP.2024.3421948.
[3]	陈涛, 邱宝传, 肖易寒, 等. 基于点云分割网络的雷达信号分选方法[J]. 电子与信息学报, 2024, 46(4): 1391–1398. doi: 10.11999/JEIT230622. CHEN Tao, QIU Baochuan, XIAO Yihan, et al. The radar signal deinterleaving method base on point cloud segmentation network[J]. Journal of Electronics & Information Technology, 2024, 46(4): 1391–1398. doi: 10.11999/JEIT230622.
[4]	MU Haiyue and QU Zhiyu. Three-dimensional DBSCAN radar radial source sorting algorithm based on TDOA and DOA information[C]. 2023 International Conference on Intelligent Communication and Networking, Changzhou, China, 2023: 154–158. doi: 10.1109/ICN60549.2023.10426191.
[5]	刘智鑫, 赵拥军. 约束准则下扩展时差直方图脉冲分选配对方法[J]. 西安电子科技大学学报, 2019, 46(6): 102–111. doi: 10.19665/j.issn1001-2400.2019.06.015. LIU Zhixin and ZHAO Yongjun. Pulse sorting and pairing based on the constrained extended TDOA histogram[J]. Journal of Xidian University, 2019, 46(6): 102–111. doi: 10.19665/j.issn1001-2400.2019.06.015.
[6]	马爽, 吴海斌, 柳征, 等. 基于递归扩展直方图的辐射源时差分选方法[J]. 国防科技大学学报, 2012, 34(5): 83–89. doi: 10.3969/j.issn.1001-2486.2012.05.017. MA Shuang, WU Haibin, LIU Zheng, et al. Method for emitter TDOA sorting based on recursive extended histogram[J]. Journal of National University of Defense Technology, 2012, 34(5): 83–89. doi: 10.3969/j.issn.1001-2486.2012.05.017.
[7]	LU Yang and DENG Zhian. A recursive sorting method based on multi-station TDOA vector[C]. The 8th International Conference on Intelligent Computing and Signal Processing, Xi'an, China, 2023: 1024–1027. doi: 10.1109/ICSP58490.2023.10248871.
[8]	马贤同, 罗景青, 孟祥豪. 基于时差的同类辐射源信号分选定位方法[J]. 电子与信息学报, 2015, 37(10): 2363–2368. doi: 10.11999/JEIT141480. MA Xiantong, LUO Jingqing, and MENG Xianghao. Signal sorting and positioning method for similar radiation sources based on time difference of arrival[J]. Journal of Electronics & Information Technology, 2015, 37(10): 2363–2368. doi: 10.11999/JEIT141480.
[9]	XIANG Zhexi, ZHOU Zou, GU Yu, et al. A multi-station signal sorting method based on time difference pair and azimuth information[M]. LIU Qi, LIU Xiaodong, CHENG Jieren, et al. Proceedings of the 12th International Conference on Computer Engineering and Networks. Singapore: Springer, 2022: 466–475. doi: 10.1007/978-981-19-6901-0_49.
[10]	ZHAO Zihao, ZHANG Huaguo, and GAN Lu. A multi-station signal sorting method based on TDOA grid clustering[C]. 2021 IEEE 6th International Conference on Signal and Image Processing, Nanjing, China, 2021: 773–778. doi: 10.1109/ICSIP52628.2021.9689025.
[11]	李松炜, 杨松岩, 邓志安, 等. 基于自适应流聚类的多站时差协同信号分选方法[J]. 信号处理, 2024, 40(4): 682–694. doi: 10.16798/j.issn.1003-0530.2024.04.007. LI Songwei, YANG Songyan, DENG Zhi’an, et al. Cooperative signal sorting method based on multi-station TDOA and adaptive stream clustering[J]. Journal of Signal Processing, 2024, 40(4): 682–694. doi: 10.16798/j.issn.1003-0530.2024.04.007.
[12]	仇洪冰, 周兰兰, 周陬, 等. 基于云模型的辐射源信号多站分选方法[J]. 电子学报, 2022, 50(10): 2469–2477. doi: 10.12263/DZXB.20210212. QIU Hongbing, ZHOU Lanlan, ZHOU Zou, et al. Multi-station sorting method for emitter signal based on cloud model[J]. Acta Electronica Sinica, 2022, 50(10): 2469–2477. doi: 10.12263/DZXB.20210212.
[13]	徐英杰, 张敏, 张文俊, 等. 对运动高重频辐射源的三星时差跟踪算法[J]. 信号处理, 2021, 37(8): 1399–1408. doi: 10.16798/j.issn.1003-0530.2021.08.007. XU Yingjie, ZHANG Min, ZHANG Wenjun, et al. The tracking algorithm of triple satellites using TDOA based on moving high pulse repetition frequency radiation emitter[J]. Journal of Signal Processing, 2021, 37(8): 1399–1408. doi: 10.16798/j.issn.1003-0530.2021.08.007.
[14]	姜宏志, 赵闯, 胡德秀, 等. 基于时差多参的单脉冲信号实时配对分选[J]. 电子学报, 2021, 49(3): 566–572. doi: 10.12263/DZXB.20191316. JIANG Hongzhi, ZHAO Chuang, HU Dexiu, et al. Real-time deinterleaving algorithm for single pulse signal based on TDOAs and multi-parameter information[J]. Acta Electronica Sinica, 2021, 49(3): 566–572. doi: 10.12263/DZXB.20191316.
[15]	LAI Yuping, YU Yiying, GUAN Wenbo, et al. A lightweight intrusion detection system using a finite dirichlet mixture model with extended stochastic variational inference[J]. IEEE Transactions on Network and Service Management, 2024, 21(4): 4701–4712. doi: 10.1109/TNSM.2024.3391250.
[16]	COUILLET R and DEBBAH M. A bayesian framework for collaborative multi-source signal sensing[J]. IEEE Transactions on Signal Processing, 2010, 58(10): 5186–5195. doi: 10.1109/TSP.2010.2052921.
[17]	WANG Zhi, CHEN Chunlin, and DONG Daoyi. A dirichlet process mixture of robust task models for scalable lifelong reinforcement learning[J]. IEEE Transactions on Cybernetics, 2023, 53(12): 7509–7520. doi: 10.1109/TCYB.2022.3170485.
[18]	HECK M, SAKTI S, and NAKAMURA S. Dirichlet process mixture of mixtures model for unsupervised subword modeling[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2018, 26(11): 2027–2042. doi: 10.1109/TASLP.2018.2852500.
[19]	KIM D, PARK J, CHUNG H C, et al. Unsupervised outlier detection using random subspace and subsampling ensembles of Dirichlet process mixtures[J]. Pattern Recognition, 2024, 156: 110846. doi: 10.1016/j.patcog.2024.110846.