基于快速无迹卡尔曼滤波的雷达高速目标追踪技术

宋佳蓁; 师卓越; 张晓平; 刘振宇

doi:10.11999/JEIT250010

基于快速无迹卡尔曼滤波的雷达高速目标追踪技术

doi: 10.11999/JEIT250010 cstr: 32379.14.JEIT250010

清华大学深圳国际研究生院深圳市 518055

基金项目: 国家自然科学基金(62388102)，深圳市科技计划(WDZC20231130080128001)

详细信息

作者简介:
宋佳蓁：女，博士生，研究方向为信号处理、统计推断

师卓越：女，硕士生，研究方向为信号处理、统计推断

张晓平：男，教授，研究方向为数据科学、信号处理、光载信息、金融科技

刘振宇：男，助理教授，研究方向为统计推断、雷达信号处理、无线通信

通讯作者:
刘振宇　zhenyuliu@sz.tsinghua.edu.cn

中图分类号: TN957.51
计量
- 文章访问数: 372
- HTML全文浏览量: 134
- PDF下载量: 43
- 被引次数: 0
出版历程
- 收稿日期: 2025-01-07
- 修回日期: 2025-05-09
- 网络出版日期: 2025-05-24
- 刊出日期: 2025-08-27

Radar High-speed Target Tracking via Quick Unscented Kalman Filter

Tsinghua Shenzhen International Graduate School, Shenzhen 518055, China

Funds: The National Natural Science Foundation of China (62388102), Shenzhen Science and Technology Program (WDZC20231130080128001)

摘要

摘要: 随着空间技术的快速发展，高速目标日益成为雷达系统追踪的重要对象。然而，高速目标的状态会在雷达一帧观测周期内发生显著变化，导致其回波信号能量在距离-多普勒量测空间中被分散，出现“跨距离单元”、“跨多普勒单元”等问题，从而极大地限制了目标追踪的精度。为解决上述问题，该文提出一种基于快速无迹卡尔曼滤波(Q-UKF)的雷达高速目标追踪技术。该技术直接使用雷达回波信号对目标状态进行逐脉冲推断，省略了传统方法中对回波信号能量的收集和校正过程，提高了追踪精度。此外，通过引入Woodbury矩阵恒等式，在与传统无迹卡尔曼滤波(UKF)算法保持相同估计精度的同时有效降低了计算复杂度。该文通过仿真实验评估了所提方法在不同目标初始状态、不同噪声类型和不同信噪比条件下的估计精度与运算效率。实验结果表明，与扩展卡尔曼滤波(EKF)算法相比，Q-UKF算法在高斯噪声及瑞利噪声环境下对目标状态的估计精度分别平均提升10.60%和9.55%，计算用时降低8.91%。同时，综合估计精度和计算效率，Q-UKF算法具有比粒子滤波(PF)算法更均衡的表现。这表明Q-UKF算法具有良好的准确性和实时性，展现了该算法的工程应用前景。
- 高速目标追踪 /
- 卡尔曼滤波 /
- 跨距离单元
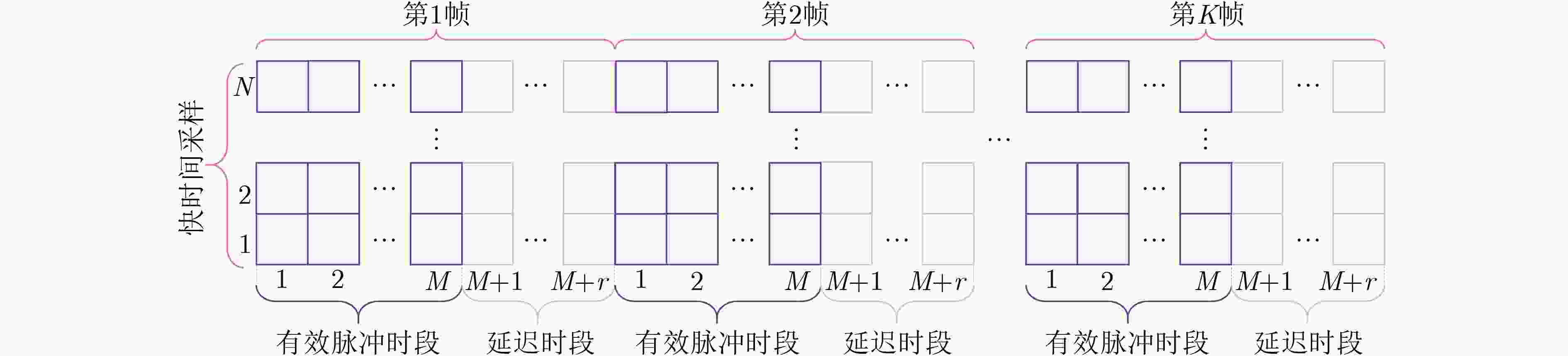
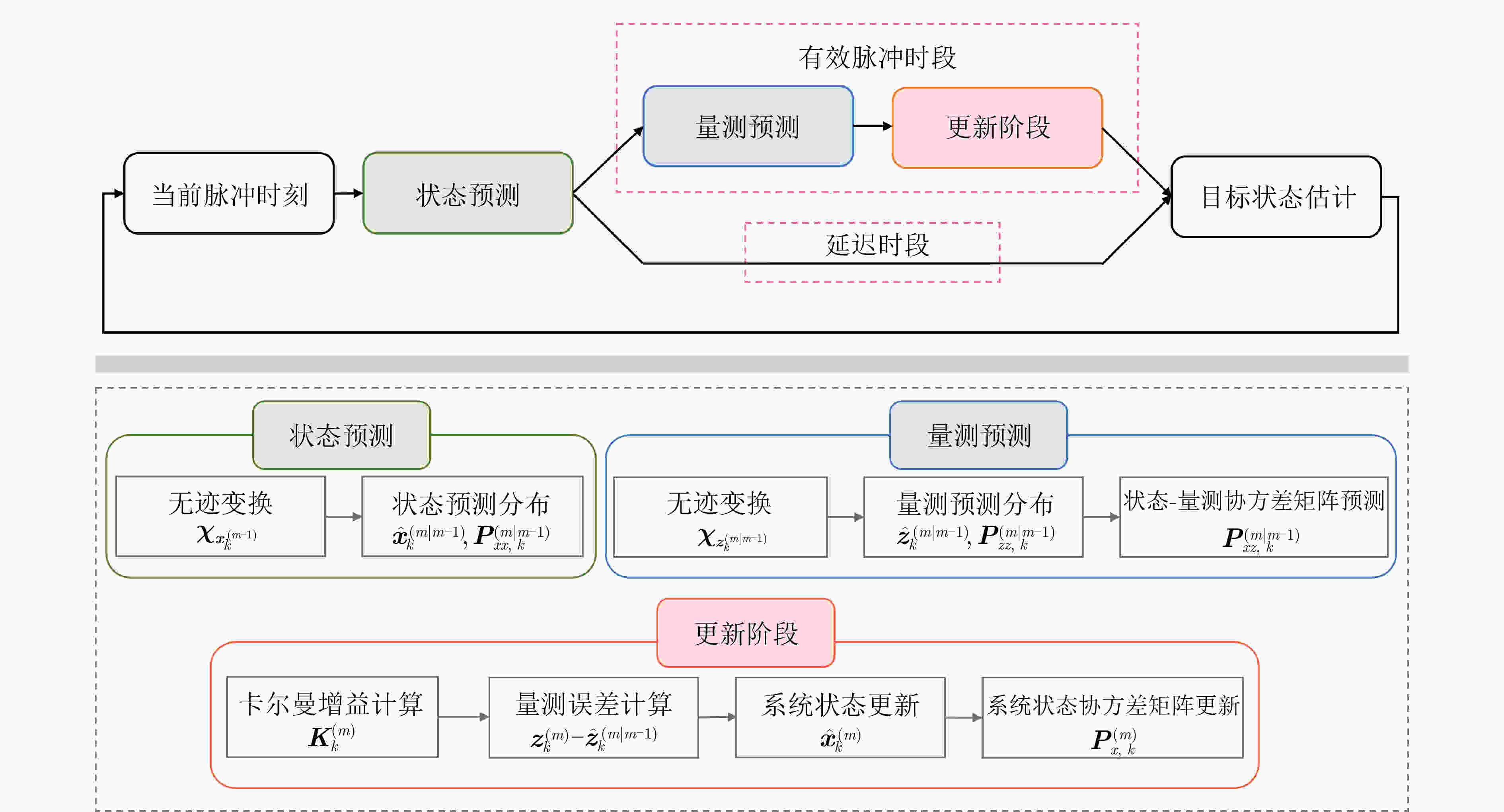
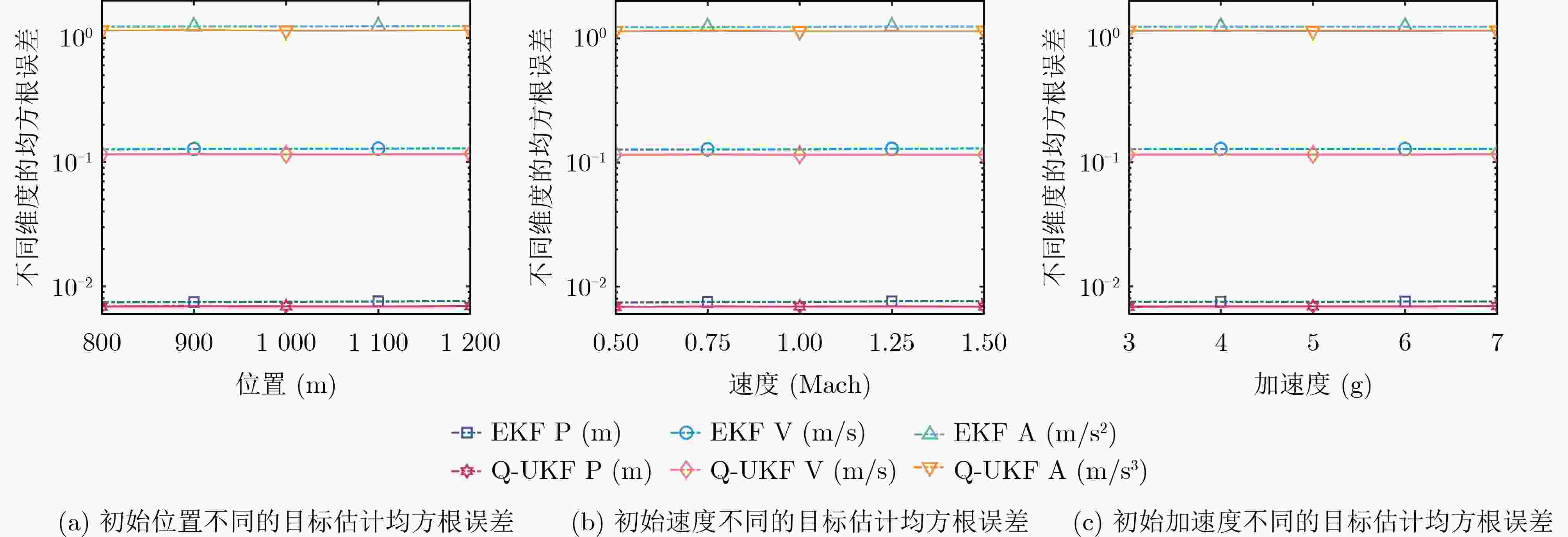
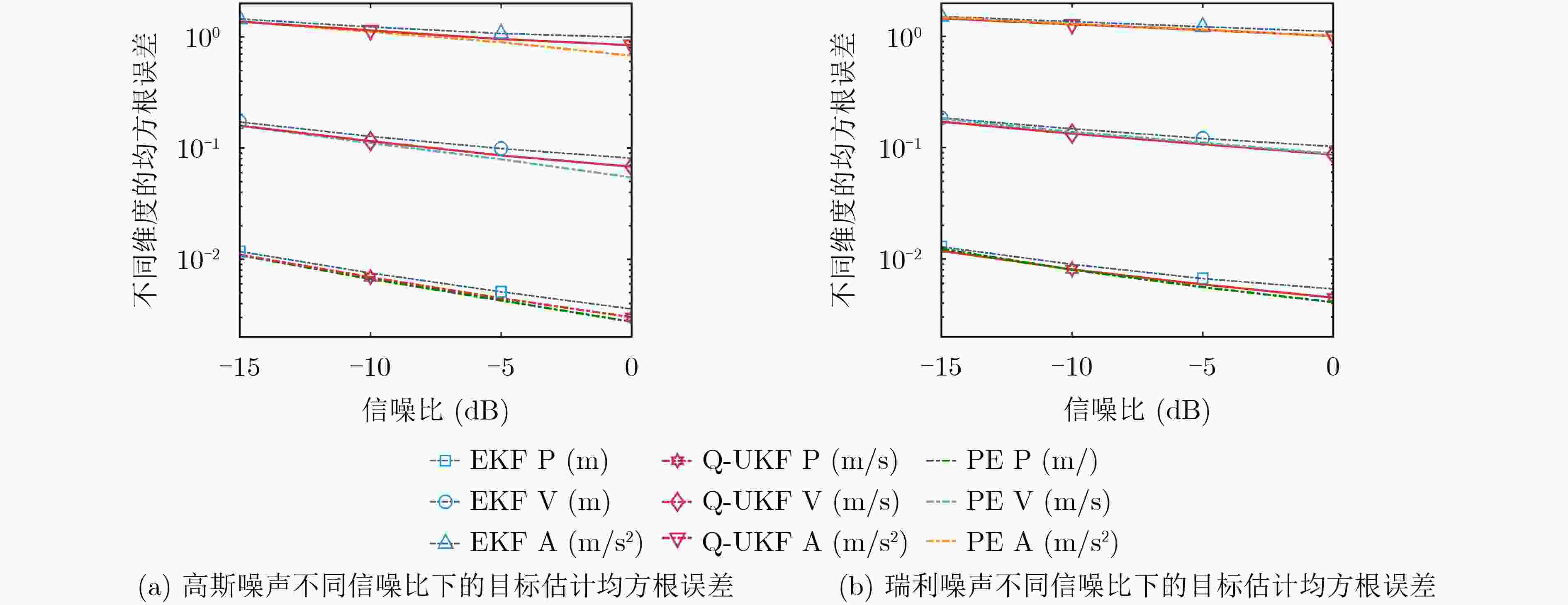
Abstract: Objective The increasing prevalence of high-speed targets due to advancements in space technology presents new challenges for radar tracking. The pronounced motion of such targets within a single frame induces large variations in range, causing dispersion of echo energy across the range-Doppler plane and invalidating the assumption of concentrated target energy. This results in “range cell migration” and “Doppler cell migration”, both of which degrade tracking accuracy. To address these challenges, this study proposes a Quick Unscented Kalman Filter (Q-UKF) algorithm tailored for high-speed radar target tracking. The Q-UKF performs recursive, pulse-by-pulse state estimation directly from radar echo signals, thereby improving tracking precision and eliminating the need for conventional energy correction and migration compensation. Furthermore, the algorithm employs the Woodbury matrix identity to reduce computational burden while preserving the estimation accuracy of the standard Unscented Kalman Filter (UKF). Methods The target state vector at each pulse time is modeled as a three-dimensional random vector representing position, velocity, and acceleration. Target motion is governed by a kinematic model that characterizes its temporal dynamics. A measurement model is formulated based on the radar echo signals received at each pulse, defining a nonlinear relationship between the target state and the observed measurements. This formulation supports recursive state estimation. In the classical UKF, the high dimensionality of radar echo data necessitates frequent inversion of large covariance matrices, imposing a substantial computational burden. To mitigate this issue, the Q-UKF is developed. By incorporating the Woodbury matrix identity, the Q-UKF reduces the computational complexity of matrix inversion without compromising estimation accuracy relative to the classical UKF. Within this framework, Q-UKF performs pulse-by-pulse recursive estimation, integrating all measurements up to the current pulse to improve prediction accuracy. In contrast to conventional radar tracking methods that process complete frame data and apply multiple signal correction steps, Q-UKF operates directly on raw measurements and avoids such corrections, thereby simplifying the processing pipeline. This efficiency makes Q-UKF well suited for real-time tracking of high-speed targets. Results and Discussions The performance of the proposed Q-UKF method is assessed using Monte Carlo simulations. Estimation errors of the Q-UKF and Extended Kalman Filter (EKF) are compared over time (Fig. 3). During the effective pulse periods within each frame cycle, both methods yield accurate target state estimates. Estimation errors increase during the delay intervals, but rapidly decrease and stabilize once effective pulse signals resume, forming a periodic error pattern. To evaluate robustness, the Root Mean Square Error (RMSE) of state estimation is examined under varied initial conditions, including different positions, velocities, and accelerations. In all scenarios, both Q-UKF and EKF perform reliably, with Q-UKF consistently demonstrating superior accuracy (Fig. 4). Under Signal-to-Noise Ratios (SNRs) from –15 dB to 0 dB, the RMSEs in both Gaussian and Rayleigh noise environments (Fig. 5a and Fig. 5b) decrease with increasing SNR. Q-UKF maintains high accuracy even under low SNR conditions. In the Gaussian noise setting, Q-UKF improves estimation accuracy by an average of 10.60% relative to EKF; in the Rayleigh environment, the average improvement is 9.55%. In terms of computational efficiency, Q-UKF demonstrates the lowest runtime among the evaluated methods (EKF, UKF, and Particle Filter (PF)). The average computation time per effective pulse is reduced by 8.91% compared to EKF, 72.55% compared to UKF, and over 90% compared to PF (Table 2). This efficiency gain results from applying the Woodbury matrix identity, which alleviates the computational load of matrix inversion in high-dimensional radar echo data processing. Conclusions This study presents the Q-UKF method for high-speed target tracking in radar systems. The algorithm performs pulse-by-pulse state estimation directly from radar echo signals, advancing estimation granularity from the frame level to the pulse level. By removing the need for energy accumulation and migration correction, Q-UKF simplifies the conventional signal processing pipeline. The method incorporates the Woodbury matrix identity to efficiently invert covariance matrices, substantially reducing computational load. Simulation results show that Q-UKF consistently outperforms the EKF in estimation accuracy under varied initial target states, achieving an average improvement of approximately 10.60% under Gaussian noise and 9.55% under Rayleigh noise. Additionally, Q-UKF improves computational efficiency by 8.91% compared to EKF. Compared to the classical UKF, Q-UKF delivers equivalent accuracy with significantly reduced runtime. Although the PF may yield slightly better accuracy under certain conditions, its computational demand limits its practicality in real-time applications. Overall, Q-UKF provides a favorable balance between accuracy and efficiency, making it a viable solution for real-time tracking of high-speed targets. Its ability to address high-dimensional, nonlinear measurement problems also highlights its potential for broader application.
- High-speed target tracking /
- Kalman filter /
- Range cell migration

HTML全文

图 1 数据帧结构图

下载: 全尺寸图片幻灯片

图 2 目标状态估计框架图

下载: 全尺寸图片幻灯片

图 3 Q-UKF算法与EKF算法估计误差随时间的变化

下载: 全尺寸图片幻灯片

图 4 Q-UKF算法与EKF算法在不同设置下的目标估计效果对比

下载: 全尺寸图片幻灯片

图 5 Q-UKF算法与EKF算法、PF算法在不同噪声设置下的估计均方根误差对比

下载: 全尺寸图片幻灯片

表 1 雷达参数设置

参数名称载波频率信号带宽脉冲重复
时间快时间
采样频率脉冲宽度

数值 0.2 GHz 20 MHz 0.005 s 20 MHz 20 μs

下载: 导出CSV

表 2 不同算法计算有效脉冲估计的运行时间对比表(ms)

算法名称 EKF UKF Q-UKF(本文算法) PF

时间 12.79 42.44 11.65 382.03

下载: 导出CSV

参考文献(27)

[1]	彭锐晖, 郭玮, 孙殿星, 等. 多平台异构信息融合的航空目标跟踪算法[J]. 电子与信息学报, 2024, 46(9): 3619–3628. doi: 10.11999/JEIT240130. PENG Ruihui, GUO Wei, SUN Dianxing, et al. Airborne target tracking algorithm using multi-platform heterogeneous information fusion[J]. Journal of Electronics & Information Technology, 2024, 46(9): 3619–3628. doi: 10.11999/JEIT240130.
[2]	WANG Shenghua, MEN Chenkai, LI Renxian, et al. A maneuvering extended target tracking IMM algorithm based on second-order EKF[J]. IEEE Transactions on Instrumentation and Measurement, 2024, 73: 8505011. doi: 10.1109/TIM.2024.3418076.
[3]	杨健, 杨文付, 谢晓阳, 等. 基于距离走动效应的SAR运动目标检测算法[J]. 太赫兹科学与电子信息学报, 2018, 16(3): 406–411. doi: 10.11805/TKYDA201803.0406. YANG Jian, YANG Wenfu, XIE Xiaoyang, et al. Moving target indication algorithm in SAR based on range walk migration[J]. Journal of Terahertz Science and Electronic Information Technology, 2018, 16(3): 406–411. doi: 10.11805/TKYDA201803.0406.
[4]	XU Aichun, ZHANG Ji, LI Qian, et al. The benefits of being smaller: Consistent pattern for climate-induced range shift and morphological difference of three falconiforme species[J]. Avian Research, 2023, 14(1): 100079. doi: 10.1016/j.avrs.2023.100079.
[5]	DENG Tiandi and JIANG Chaoshu. Evaluations of keystone transforms using several interpolation methods[C]. 2011 IEEE CIE International Conference on Radar, Chengdu, China, 2011: 1876–1878. doi: 10.1109/CIE-Radar.2011.6159939.
[6]	张亮, 张翔宇, 王国宏. Keystone变换实现方法研究[J]. 电子学报, 2022, 50(5): 1218–1226. doi: 10.12263/DZXB.20210464. ZHANG Liang, ZHANG Xiangyu, and WANG Guohong. Research on keystone transform implementation methods[J]. Acta Electronica Sinica, 2022, 50(5): 1218–1226. doi: 10.12263/DZXB.20210464.
[7]	PIGNOL F, COLONE F, and MARTELLI T. Lagrange-polynomial-interpolation-based Keystone transform for a passive radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(3): 1151–1167. doi: 10.1109/TAES.2017.2775924.
[8]	JIANG Wenqi, LIU Hongwei, JIU Bo, et al. Full-dimensional partial-search generalized radon-Fourier transform for high-speed maneuvering target detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2024, 60(4): 5445–5457. doi: 10.1109/TAES.2024.3393449.
[9]	LI Xiaolong, ZHANG Zerui, YANG Fan, et al. Motion error estimation and coherent integration for high-speed target with airborne bistatic radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2024: 1–19. doi: 10.1109/TAES.2024.3520537.
[10]	NIU Zhiyong, ZHENG Jibin, SU Tao, et al. Radar high-speed target detection based on improved minimalized windowed RFT[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 870–886. doi: 10.1109/JSTARS.2020.3037089.
[11]	LI Xiaolong, CUI Guolong, KONG Lingjiang, et al. Fast Non-searching method for maneuvering target detection and motion parameters estimation[J]. IEEE Transactions on Signal Processing, 2016, 64(9): 2232–2244. doi: 10.1109/TSP.2016.2515066.
[12]	LI Xiaolong, SUN Zhi, YI Wei, et al. Radar detection and parameter estimation of high-speed target based on MART-LVT[J]. IEEE Sensors Journal, 2019, 19(4): 1478–1486. doi: 10.1109/JSEN.2018.2882198.
[13]	JIN Pan, RAO Xuan, ZHU Xiangsheng, et al. Weak target integration detection based on bistatic radar second-order keystone transform[C]. 2019 IEEE International Conference on Signal, Information and Data Processing, Chongqing, China, 2019: 1–6. doi: 10.1109/ICSIDP47821.2019.9173183.
[14]	YANG Jiefang, ZHANG Yunhua, MI Yunpeng, et al. A novel algorithm for maneuvering target coherent integration based on second-order keystone and radon Fourier transform[C]. IET International Radar Conference (IRC 2023), Chongqing, China, 2023: 2458–2463. doi: 10.1049/icp.2024.1472.
[15]	SUN Zhi, LI Xiaolong, CUI Guolong, et al. A fast approach for detection and parameter estimation of maneuvering target with complex motions in coherent radar system[J]. IEEE Transactions on Vehicular Technology, 2021, 70(10): 10278–10292. doi: 10.1109/TVT.2021.3104659.
[16]	HUANG Penghui, XIA Xianggen, LIAO Guisheng, et al. Long-time coherent integration algorithm for radar maneuvering weak target with acceleration rate[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(6): 3528–3542. doi: 10.1109/TGRS.2018.2885508.
[17]	肖培. 地基雷达高速目标检测技术研究[D]. [硕士论文], 电子科技大学, 2019. XIAO Pei. Research on ground-based radar high-speed target detection technology[D]. [Master dissertation], University of Electronic Science and Technology of China, 2019.
[18]	BASAR T. A new approach to linear filtering and prediction problems[M]. BASAR T. Control Theory: Twenty-Five Seminal Papers. Hoboken: Wiley-IEEE Press, 2001: 167–179. doi: 10.1109/9780470544334.ch9.
[19]	KALMAN R E and BUCY R S. New results in linear filtering and prediction theory[J]. Journal of Basic Engineering, 1961, 83(1): 95–108. doi: 10.1115/1.3658902.
[20]	JULIER S J and UHLMANN J K. New extension of the Kalman filter to nonlinear systems[C]. Signal Processing, Sensor Fusion, and Target Recognition VI, Orlando, USA, 1997: 182–193.
[21]	ARULAMPALAM M S, MASKELL S, GORDON N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Transactions on Signal Processing, 2002, 50(2): 174–188. doi: 10.1109/78.978374.
[22]	ARASARATNAM I and HAYKIN S. Cubature Kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254–1269. doi: 10.1109/TAC.2009.2019800.
[23]	DUNIK J, STRAKA O, SIMANDL M, et al. Random-point-based Filters: Analysis and comparison in target tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(2): 1403–1421. doi: 10.1109/TAES.2014.130136.
[24]	计忠平, 王相威, 何志伟, 等. 集成全局局部特征交互与角动量机制的端到端多目标跟踪算法[J]. 电子与信息学报, 2024, 46(9): 3703–3712. doi: 10.11999/JEIT240277. JI Zhongping, WANG Xiangwei, HE Zhiwei, et al. End-to-end multi-object tracking algorithm integrating global local feature interaction and angular momentum mechanism[J]. Journal of Electronics & Information Technology, 2024, 46(9): 3703–3712. doi: 10.11999/JEIT240277.
[25]	程稳, 陈忠碧, 李庆庆, 等. 时空特征对齐的多目标跟踪算法[J]. 光电工程, 2023, 50(6): 230009. doi: 10.12086/oee.2023.230009. CHENG Wen, CHEN Zhongbi, LI Qingqing, et al. Multiple object tracking with aligned spatial-temporal feature[J]. Opto-Electronic Engineering, 2023, 50(6): 230009. doi: 10.12086/oee.2023.230009.
[26]	刘超军, 段喜萍, 谢宝文. 应用GhostNet卷积特征的ECO目标跟踪算法改进[J]. 激光技术, 2022, 46(2): 239–247. doi: 10.7510/jgjs.issn.1001-3806.2022.02.015. LIU Chaojun, DUAN Xiping, and XIE Baowen. Improvement of ECO target tracking algorithm based on GhostNet convolution feature[J]. Laser Technology, 2022, 46(2): 239–247. doi: 10.7510/jgjs.issn.1001-3806.2022.02.015.
[27]	吴非, 张建林. 结合全局光流的孪生区域提名网络目标跟踪算法[J]. 半导体光电, 2023, 44(3): 422–428. doi: 10.16818/j.issn1001-5868.2023020401. WU Fei and ZHANG Jianlin. Siamese region proposal network object tracking algorithm with global optical flow[J]. Semiconductor Optoelectronics, 2023, 44(3): 422–428. doi: 10.16818/j.issn1001-5868.2023020401.