Bootstrapping Optimization Techniques for the FINAL Fully Homomorphic Encryption Scheme
-
摘要: 自举是实现全同态加密的有效方法，同时也是影响全同态加密效率的关键环节。FINAL方案是2022年亚密会提出的全同态密码方案，比TFHE方案自举速度快28%，可以进行高效的同态布尔运算。自举主要包括盲旋转算法和密钥转换算法。针对盲旋转算法，该文提出累加器压缩方法，即对基于容错学习(LWE)的加密方案的密钥生成引入块二进制分布，利用块二进制密钥特性，使得密钥的每个分块只需进行1次外积运算，减少盲旋转算法所需的外积数量。针对密钥转换算法，给出了密钥复用技术，即在生成NGS密钥时复用LWE密钥且复用部分不参与密钥转换的密钥生成，减小了密钥转换密钥规模，进而减少密钥转换算法运算次数，提高了密钥转换算法的效率。分析表明，在安全性相当的情况下，优化的FINAL方案自举所需要执行的外积数量和快速傅里叶变换的数量分别由610和3 940减少到305和1 970，数量上优化50%。密钥转换密钥规模由11 264减少到4 554，密钥转换中标量乘法以及标量加法的运算次数大约由13.8×106减少到5.6×106，密钥转换的密钥规模和计算开销均优化约60%。Abstract:
Objective Bootstrapping is a fundamental process in Fully Homomorphic Encryption (FHE) that directly affects its practical efficiency. The FINAL scheme, presented at ASIACRYPT 2022, achieves a 28% improvement in bootstrapping speed compared with TFHE, demonstrating high suitability for homomorphic Boolean operations. Nevertheless, further improvements are required to reduce its computational overhead and storage demands. This study aims to optimize the bootstrapping phase of FINAL by lowering its computational complexity and key size while preserving the original security level. Methods This study proposes two key optimizations. Accumulator compression for blind rotation: A blockwise binary distribution is incorporated into the Learning With Errors (LWE) key generation process. By organizing the key into blocks, each requiring only a single external product, the number of external product operations during blind rotation is reduced. Key reuse strategy for key switching: The LWE key is partially reused during the generation of the Number-theoretic Gadget Switching (NGS) key. The reused portion is excluded from the key switching key, thereby reducing both the key size and the number of associated operations. Results and Discussions Under equivalent security assumptions, the optimized FINAL scheme yields substantial efficiency gains. For blind rotation, the number of external product operations is reduced by 50% (from 610 to 305), and the number of Fast Fourier Transform (FFT) operations is halved (from 3,940 to 1,970) ( Table 5 ). For key switching, the key size is reduced by 60% (from 11,264 to 4,554), and the computational complexity decreases from 13.8 × 106 to 5.6× 106 scalar operations (Table 6 ).Conclusions The proposed optimizations substantially improve the efficiency of the FINAL scheme’s bootstrapping phase. Blind rotation benefits from structured key partitioning, reducing the number of core operations by half. Key switching achieves comparable reductions in both storage requirements and computational cost through partial key reuse. These enhancements improve the practicality of FHE for real-world applications that demand efficient evaluation of Boolean circuits. Future directions include hardware acceleration and adaptive parameter tuning. -
Key words:
- Fully Homomorphic Encryption (FHE) /
- FINAL /
- Bootstrapping /
- Blind rotation /
- Key switching
-
1 自举算法
输入：盲旋转密钥BRK， 加密消息为$m$的LWE密文${\boldsymbol{c}} = (b,{\boldsymbol{a}}) \in \mathbb{Z}_q^{n + 1}$， 密钥转换密钥${\text{ks}}{{\text{k}}_{{\text{NTRU}} \to {\text{LWE}}}}$。 输出：新的LWE密文${\boldsymbol{c}}'$，加密消息为$m$。 (1) $ \left\lceil {2N\cdot {\boldsymbol{c}}/q} \right\rfloor =(\bar b,\bar a_0,\bar a_1,\cdots,\bar a_{n-1})$ (2) $ {\mathrm{ACC}}\leftarrow\left\lceil {Q/8} \right\rfloor\cdot X^{(N/2)+\bar b} \cdot \displaystyle\sum\nolimits_{i=0}^{N-1}X^i $ (3) for $0 \le j < n$ do (4) ${\text{ACC}} \leftarrow {\text{ACC}} + {\text{[ACC}} \cdot ({X^{{{\bar a}_j}}} - 1){\text{]}} \odot {\text{BR}}{{\text{K}}_i}$ (4) (5)end for (6) $ {\mathrm{ACC}}\leftarrow {\mathrm{ACC}}+\left\lceil{Q/8} \right\rfloor \cdot \displaystyle\sum\nolimits_{i=0}^{N-1}X^i $ (7) ${\text{ACC}} \leftarrow {\text{ModSwitch}}({\text{ACC}})$ (8) ${\boldsymbol{c}}' \leftarrow {\text{KeySwitc}}{{\text{h}}_{{\text{NTRU}} \to {\text{LWE}}}}({\text{ACC}},{\text{ks}}{{\text{k}}_{{\text{NTRU}} \to {\text{LWE}}}})$ (9) return ${\boldsymbol{c}}'$ 
下载: 导出CSV
2 NewBlindRotate$ ({\text{BRK}},{\boldsymbol{c}})$
输入：盲旋转密钥BRK和一个LWE密文${\boldsymbol{c}} = (b,{\boldsymbol{a}}) \in \mathbb{Z}_q^{n + 1}$ 输出：NTRU(NGS)密文$c = g/f + \epsilon + \varDelta {{\cdot m}} \in {R_{{q}}} $ (1) $ \left\lceil {2N\cdot {\boldsymbol{c}}/q} \right\rfloor =(\bar b,\bar a_0,\bar a_1,\cdots,\bar a_{n-1})$ (2) $ {\mathrm{ACC}}\leftarrow\left\lceil {Q/8} \right\rfloor\cdot X^{(N/2)+\bar b} \cdot \displaystyle\sum\nolimits_{i=0}^{N-1}X^i$ (3) for $0 \le j < k$ do (4) $ {\text{ACC}} \leftarrow {\text{ACC}} + {\text{ACC}} \odot [\mathop \sum \nolimits_{i \in {I_j}} ({X^{{{\bar a}_i}}} - 1) \cdot {\text{BR}}{{\text{K}}_i}] $ (6) (5) end for (6) return ACC
下载: 导出CSV
表 1 盲旋转算法的性能分析
方案 FFT 标量乘法 FINAL[14] $(\ell + 1) \cdot n$ $\ell \cdot N\cdot n$ 本文方案 $(\ell + 1) \cdot k$ $\ell \cdot N\cdot n$
下载: 导出CSV
表 2 密钥转换的性能分析
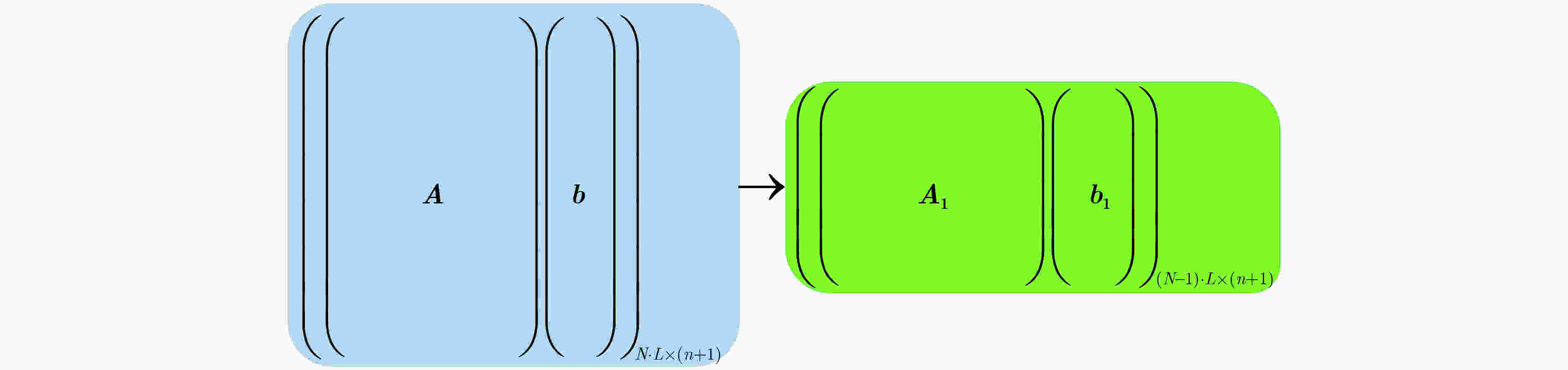
方案 标量乘法 标量加法 密钥转换密钥 FINAL[14] $N \cdot L \cdot (n + 1)$ $(N \cdot L - 1) \cdot (n + 1)$ $N \cdot L$ 本文方案 $(N - n) \cdot L \cdot (n + 1) + n$ $((N - n) \cdot L - 1) \cdot (n + 1) + n$ $(N - n) \cdot L$
下载: 导出CSV
3 NewBoot(BRK,${\text{ks}}{{\text{k}}_{{\text{NTRU}} \to {\text{LWE}}}},{\boldsymbol{c}}{\text{)}}$
输入： 盲旋转密钥BRK，密钥转换密钥${\text{ks}}{{\text{k}}_{{\text{NTRU}} \to {\text{LWE}}}}$， LWE
密文${\boldsymbol{c}} = (b,{\boldsymbol{a}}) \in \mathbb{Z}_q^{n + 1}$。输出： LWE密文${\boldsymbol{c}}' \in \mathbb{Z}_q^{n + 1}$。 (1) ${\text{ACC}} \leftarrow {\text{NewBlindRotate}}({\text{BRK}},{\boldsymbol{c}})$ (2) ACC$\leftarrow {\mathrm{AAC}}+\left\lceil {Q/8} \right\rfloor \cdot \displaystyle\sum\nolimits_{i=0}^{N-1}X^i $ (3) ${\text{ACC}} \leftarrow {\text{ModSwitch}}({\text{ACC}})$ (4) ${\boldsymbol{c}}' \leftarrow {\text{NewKeySwitc}}{{\text{h}}_{{\text{NTRU}} \to {\text{LWE}}}}({\text{ks}}{{\text{k}}_{{\text{NTRU}} \to {\text{LWE}}}},{\text{ACC}})$
下载: 导出CSV
表 3 安全性分析
n N l k q MitM Primal Dual 610 1 024 1 610 92 683 170 125 134 610 1 024 2 305 92 683 135 124 131 610 1 024 3 204 92 683 113 123 129 610 1 024 4 153 92 683 98 122 128 610 1 024 5 122 92 683 88 121 126
下载: 导出CSV
-
[1] GENTRY C. Fully homomorphic encryption using ideal lattices[C]. The Forty-First Annual ACM Symposium on Theory of Computing, Bethesda, USA, 2009: 169–178. doi: 10.1145/1536414.1536440. [2] BRAKERSKI Z, GENTRY C, and VAIKUNTANATHAN V. (Leveled) fully homomorphic encryption without bootstrapping[J]. ACM Transactions on Computation Theory (TOCT), 2014, 6(3): 13. doi: 10.1145/2633600. [3] BRAKERSKI Z. Fully homomorphic encryption without modulus switching from classical GapSVP[C]. The 32nd Annual Cryptology Conference on Advances in Cryptology, Santa Barbara, USA, 2012: 868–886. doi: 10.1007/978-3-642-32009-5_50. [4] FAN Junfeng and VERCAUTEREN F. Somewhat practical fully homomorphic encryption[EB/OL]. https://eprint.iacr.org/2012/144, 2012. [5] GENTRY C, SAHAI A, and WATERS B. Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based[C]. The 33rd Annual Cryptology Conference on Advances in Cryptology, Santa Barbara, USA, 2013: 75–92. doi: 10.1007/978-3-642-40041-4_5. [6] CHEON J H, KIM A, KIM M, et al. Homomorphic encryption for arithmetic of approximate numbers[C]. The 23rd International Conference on the Theory and Applications of Cryptology and Information Security Advances in Cryptology, Hong Kong, China, 2017: 409–437. doi: 10.1007/978-3-319-70694-8_15. [7] DUCAS L and MICCIANCIO D. FHEW: Bootstrapping homomorphic encryption in less than a second[C]. The 34th Annual International Conference on the Theory and Applications of Cryptographic Techniques Advances in Cryptology, Sofia, Bulgaria, 2015: 617–640. doi: 10.1007/978-3-662-46800-5_24. [8] CHILLOTTI I, GAMA N, GEORGIEVA M, et al. TFHE: Fast fully homomorphic encryption over the torus[J]. Journal of Cryptology, 2020, 33(1): 34–91. doi: 10.1007/s00145-019-09319-x. [9] CARPOV S, IZABACHÈNE M, and MOLLIMARD V. New techniques for multi-value input homomorphic evaluation and applications[C]. The Cryptographers’ Track at the RSA Conference 2019 Topics in Cryptology, San Francisco, USA, 2019: 106–126. doi: 10.1007/978-3-030-12612-4_6. [10] CHILLOTTI I, LIGIER D, ORFILA J B, et al. Improved programmable bootstrapping with larger precision and efficient arithmetic circuits for TFHE[C]. The 27th International Conference on the Theory and Application of Cryptology and Information Security Advances in Cryptology, Singapore, Singapore, 2021: 670–699. doi: 10.1007/978-3-030-92078-4_23. [11] GUIMARÃES A, BORIN E, and ARANHA D F. Revisiting the functional bootstrap in TFHE[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2021, 2021(2): 229–253. doi: 10.46586/tches.v2021.i2.229-253. [12] CHEN Hao, CHILLOTTI I, and SONG Y. Multi-key homomorphic encryption from TFHE[C]. The 25th International Conference on the Theory and Application of Cryptology and Information Security Advances in Cryptology, Kobe, Japan, 2019: 446–472. doi: 10.1007/978-3-030-34621-8_16. [13] KWAK H, MIN S, and SONG Y. Towards practical multi-key TFHE: Parallelizable, key-compatible, quasi-linear complexity[C]. The 27th IACR International Conference on Practice and Theory of Public-Key Cryptography Public-Key Cryptography, Sydney, Australia, 2024: 354–385. doi: 10.1007/978-3-031-57728-4_12. [14] BONTE C, ILIASHENKO I, PARK J, et al. FINAL: Faster FHE instantiated with NTRU and LWE[C]. The 28th International Conference on the Theory and Application of Cryptology and Information Security Advances in Cryptology, Taipei, China, 2022: 188–215. doi: 10.1007/978-3-031-22966-4_7. [15] KLUCZNIAK K. NTRU-v-um: Secure fully homomorphic encryption from NTRU with small modulus[C]. The 2022 ACM SIGSAC Conference on Computer and Communications Security, Los Angeles, USA, 2022: 1783–1797. doi: 10.1145/3548606.3560700. [16] LEE Y, MICCIANCIO D, KIM A, et al. Efficient FHEW bootstrapping with small evaluation keys, and applications to threshold homomorphic encryption[C]. The 42nd Annual International Conference on the Theory and Applications of Cryptographic Techniques Advances in Cryptology, Lyon, France, 2023: 227–256. doi: 10.1007/978-3-031-30620-4_8. [17] LEE C, MIN S, SEO J, et al. Faster TFHE bootstrapping with block binary keys[C]. The 2023 ACM Asia Conference on Computer and Communications Security, Melbourne, Australia, 2023: 2–13. doi: 10.1145/3579856.3595804. [18] XIANG Binwu, ZHANG Jiang, DENG Yi, et al. Fast blind rotation for bootstrapping FHEs[C]. The 43rd Annual International Cryptology Conference on Advances in Cryptology, Santa Barbara, USA, 2023: 3–36. doi: 10.1007/978-3-031-38551-3_1. [19] MA Shihe, HUANG Tairong, WANG Anyu, et al. Accelerating BGV bootstrapping for large p using null polynomials over $ \mathbb{Z}_{p^{e}} $[C]. The 43rd Annual International Conference on the Theory and Applications of Cryptographic Techniques Advances in Cryptology, Zurich, Switzerland, 2024: 403–432. doi: 10.1007/978-3-031-58723-8_14. [20] WANG Ruida, WEN Yundi, LI Zhihao, et al. Circuit bootstrapping: Faster and smaller[C]. The 43rd Annual International Conference on the Theory and Applications of Cryptographic Techniques Advances in Cryptology, Zurich, Switzerland, 2024: 342–372. doi: 10.1007/978-3-031-58723-8_12. [21] PEIKERT C. A decade of lattice cryptography[J]. Foundations and Trends® in Theoretical Computer Science, 2016, 10(4): 283–424. doi: 10.1561/0400000074. [22] GOLDWASSER S, KALAI Y, PEIKERT C, et al. Robustness of the learning with errors assumption[C]. Proceedings of the Innovations in Computer Science–ICS 2010, Beijing, China, 2010: 230–240. [23] ALBRECHT M R. On dual lattice attacks against small-secret LWE and parameter choices in HElib and SEAL[C]. The 36th Annual International Conference on the Theory and Applications of Cryptographic Techniques Advances in Cryptology, Paris, France, 2017: 103–129. doi: 10.1007/978-3-319-56614-6_4. [24] MAY A. How to meet ternary LWE keys[C]. The 41st Annual International Cryptology Conference on Advances in Cryptology, 2021: 701–731. doi: 10.1007/978-3-030-84245-1_24. [25] ALBRECHT M R, PLAYER R, and SCOTT S. On the concrete hardness of Learning with Errors[J]. Journal of Mathematical Cryptology, 2015, 9(3): 169–203. doi: 10.1515/jmc-2015-0016. [26] CHEN Yuanmi and NGUYEN P Q. BKZ 2.0: Better lattice security estimates[C]. The 17th International Conference on the Theory and Application of Cryptology and Information Security Advances in Cryptology, Seoul, South Korea, 2011: 1–20. doi: 10.1007/978-3-642-25385-0_1. [27] GUO Qian and JOHANSSON T. Faster dual lattice attacks for solving LWE with applications to CRYSTALS[C]. The 27th International Conference on the Theory and Application of Cryptology and Information Security Advances in Cryptology, Singapore, Singapore, 2021: 33–62. doi: 10.1007/978-3-030-92068-5_2. -
图(3) / 表(9)
计量
- 文章访问数: 202
- HTML全文浏览量: 117
- PDF下载量: 34
- 被引次数: 0
下载:
