Secure Transmission Scheme for Reconfigurable Intelligent Surface-enabled Cooperative Simultaneous Wireless Information and Power Transfer Non-Orthogonal Multiple Access System
-
摘要: 可重构智能超表面(RIS)因能提供额外的无源波束增益被视为一项颇具前景的技术。考虑到未来大型物联网中不同用户服务需求的多样性及信息传输的安全性,该文面向协作无线携能同传-非正交多址接入(SWIPT-NOMA)系统,提出一种RIS使能的安全传输方案。通过合理部署RIS的位置,将其同时作用于直接传输阶段和协作传输阶段。在满足非正交多址接入(NOMA)弱用户信息速率需求、NOMA强用户能量收集需求和基站最小发射功率的条件下,通过联合优化基站的有源波束成形、RIS的相移矩阵、强用户的功率分割系数等来最大化强用户的保密速率。为解决所提的多变量耦合的非凸优化问题,该文基于交替迭代优化算法,对基站的有源波束成形、直接传输阶段的RIS无源波束相移矩阵、协作传输阶段的RIS有源波束相移矩阵以及强用户的功率分割系数等进行了多次交替迭代优化,直至算法收敛。仿真结果验证了该文算法的收敛性,且与其它基准方案相比,所提方案可进一步提高强用户的保密速率。Abstract:
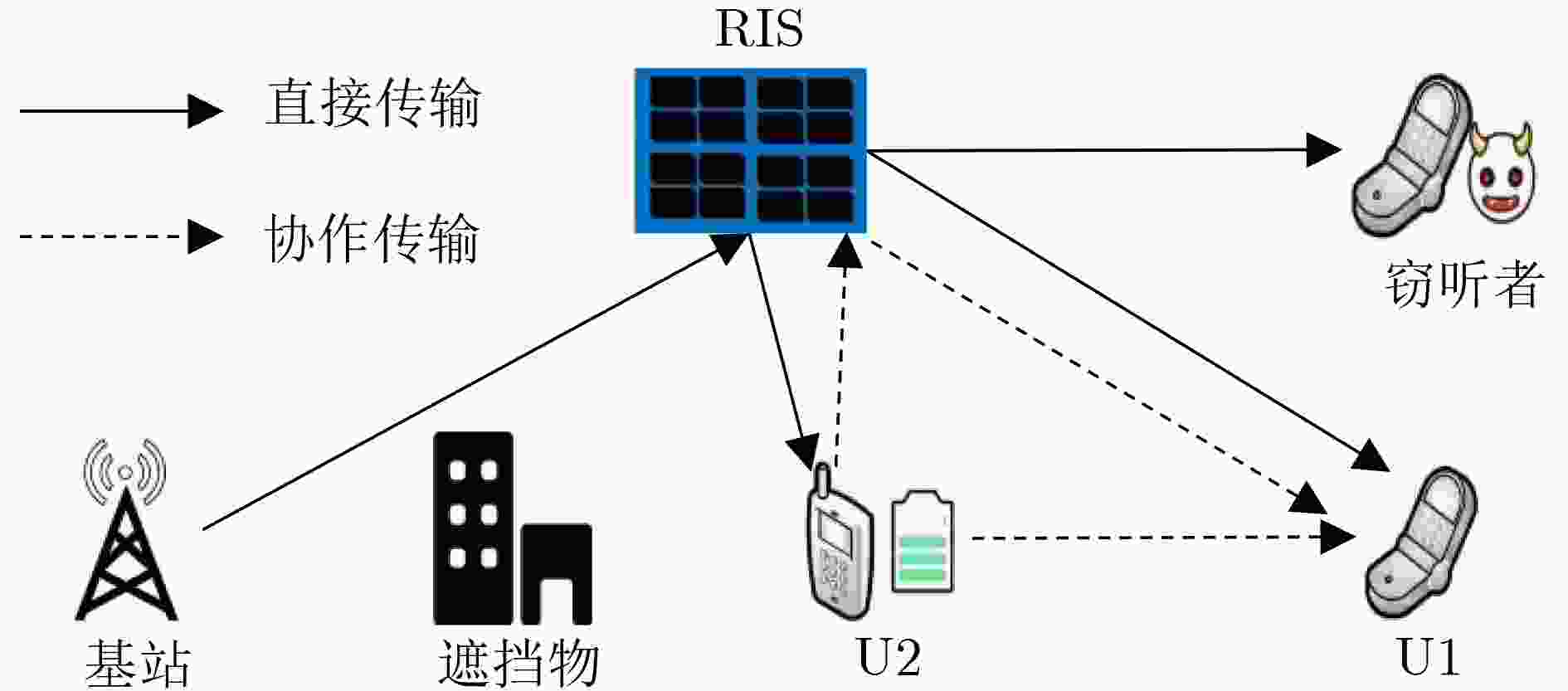
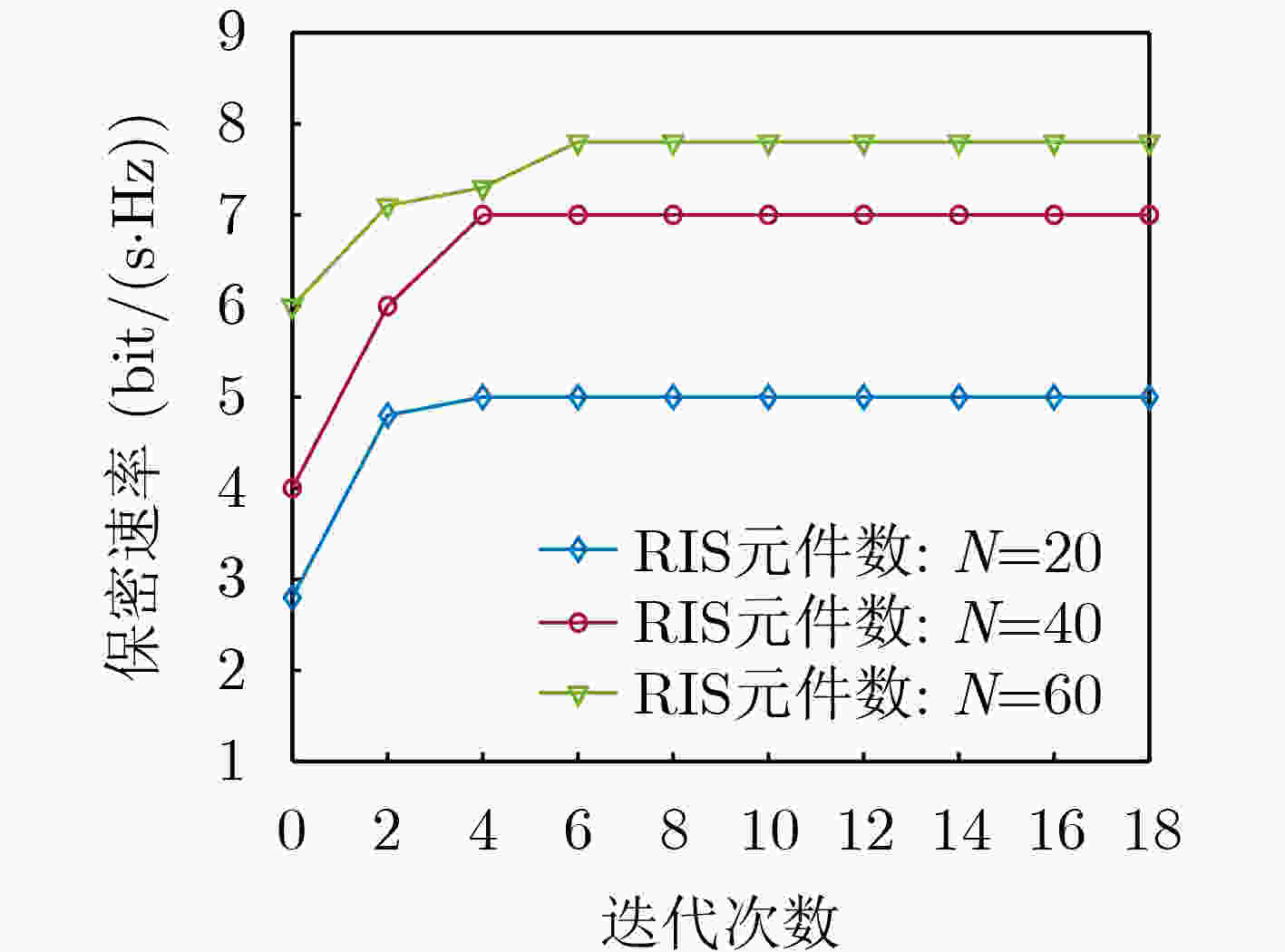
Objective The Reconfigurable Intelligent Surface (RIS) is emerging as a promising technology due to its ability to provide passive beamforming gains, which can be seamlessly integrated into existing wireless networks without altering physical layer standards. The integration of RIS with other advanced technologies offers new opportunities for communication network design. In the context of future large-scale Internet of Things (IoT) systems, users are expected to have diverse requirements. These differences in structure and function lead to two distinct receiver operation modes: Power Splitting (PS) and Time Switching (TS). Furthermore, users’ service needs may vary, including energy harvesting and information transmission. In practice, IoT terminals often face energy constraints. Additionally, the network typically operates in an open wireless environment, where the inherent broadcasting nature of wireless channels may introduce security vulnerabilities. To address the diverse service demands in large-scale IoT networks and ensure secure information transmission, this study proposes an RIS-enabled secure transmission scheme for a cooperative Simultaneous Wireless Information and Power Transfer Non-Orthogonal Multiple Access (SWIPT-NOMA) system. Methods The RIS is strategically deployed to assist transmission during both the direct and cooperative transmission stages. The goal is to maximize the secrecy rate of the strong NOMA user, subject to the information rate requirements of the weak NOMA user, the energy harvesting needs of the strong NOMA user, and the base station’s minimum transmission power. To solve this multivariable-coupled, non-convex optimization problem, an alternating iterative optimization algorithm is applied. The algorithm optimizes the base station’s active beamforming, the RIS’s passive beam phase shift matrix in the direct transmission stage, the RIS’s active beam phase shift matrix in the cooperative transmission stage, and the PS coefficient of the strong user. These parameters are iteratively adjusted until convergence is achieved. Results and Discussions The convergence of the algorithm is demonstrated in ( Fig. 3 ). As the number of RIS components increases and the number of iterations grows, the secrecy rate of the strong user (U2) gradually improves until it converges. To evaluate the effectiveness of the proposed scheme, it is compared with several benchmark schemes: (1) The random PS coefficient scheme, where RIS is used in both the direct and cooperative transmission stages, and the PS coefficients for strong user U2 are randomly generated. (2) The random RIS phase shift matrix scheme, where RIS enables both transmission stages, with phase shift matrices for both stages randomly generated. (3) The SDR scheme, in which RIS is used in both transmission stages, and the phase shift matrices are optimized using the SDR method. (4) The RIS-enabled direct transmission scheme, where RIS is used only in the direct transmission stage. The impact of the number of base station antennas on the system’s secrecy rate is shown in (Fig. 4 ), and the effect of the number of RIS components on the secrecy rate is explored in (Fig. 5 ). Compared to the other baseline schemes, the proposed scheme achieves a higher secrecy rate for the strong user.Conclusions This paper addresses the challenge of diverse service requirements for users in future large-scale IoT networks and the security of information transmission by designing a secure transmission scheme for an RIS-enabled cooperative SWIPT-NOMA communication system. RIS assists communication in both the direct and cooperative transmission stages. The secrecy rate of the strong user is maximized while considering the information rate requirements of weak NOMA users, the energy harvesting needs of strong NOMA users, and the base station’s minimum transmission power. The proposed optimization problem is a non-convex, multi-variable problem, which is difficult to solve directly. To address this, the problem is divided into several sub-problems, and the active beamforming of the base station, the passive beam phase shift matrix of the RIS in the direct transmission stage, the active beam phase shift matrix of the RIS in the cooperative transmission stage, and the power splitting coefficient of the strong user are iteratively optimized until convergence. Simulation results demonstrate that the secrecy rate of the proposed scheme outperforms that of the scheme where RIS is enabled only in the direct transmission stage. Compared to other baseline schemes, the proposed scheme further enhances the secrecy rate for strong users. -
1 基站有源波束成形子问题求解算法
令$ i = 0 $,初始化可行解$ {\boldsymbol{W}}_1^{(i)},\;{\boldsymbol{W}}_2^{(i)} $,辅助变量$ x_1^{(i)} $ for 交替更新求解 已知$ {\boldsymbol{W}}_1^{(i)},\;{\boldsymbol{W}}_2^{(i)} $,计算$ {t^{(i + 1)}} $ 已知$ {\boldsymbol{W}}_1^{(i)},\;{\boldsymbol{W}}_2^{(i)},\;x_1^{(i)} $, 计算$ {a^{(i + 1)}} $ 已知$ {t^{(i + 1)}},{a^{(i + 1)}} $,求解问题P2,获得${\boldsymbol{W}}_1^{(i + 1)},\;{\boldsymbol{W}}_2^{(i + 1)} $,
$ x_1^{(i + 1)} $更新$ i = i + 1 $ end for:收敛 输出基站有源波束成形矩阵$ {\boldsymbol{W}}_1^{(i)},\;{\boldsymbol{W}}_2^{(i)} $,辅助变量$ x_1^{(i)} $ 2 直接传输阶段RIS无源波束成形优化子问题求解算法
令$ i = 0 $,初始化可行解$ {\boldsymbol{Q}}_1^{(i)} $,辅助变量$ x_2^{(i)} $ for 交替更新求解 已知$ {\boldsymbol{Q}}_1^{(i)} $,计算$ {z^{(i + 1)}} $ 已知$ {\boldsymbol{Q}}_1^{(i)},\;x_2^{(i)} $, 计算$ {b^{(i + 1)}} $ 已知$ {z^{(i + 1)}},{b^{(i + 1)}} $,求解问题P4,获得$ {\boldsymbol{Q}}_1^{(i + 1)},x_2^{(i + 1)} $ 更新$ i = i + 1 $ end for:收敛 输出基站有源波束成形矩阵$ {\boldsymbol{Q}}_1^{(i)} $,辅助变量$ x_2^{(i)} $ 3 基于交替迭代的整体算法
令$ i = 0 $,初始化可行解$ {\boldsymbol{w}}_1^{(i)},{\boldsymbol{w}}_2^{(i)},{\boldsymbol{Q}}_1^{(i)},{\boldsymbol{Q}}_2^{(i)},{\rho ^{(i)}} $ for 交替更新求解$ {{\boldsymbol{w}}_1},{{\boldsymbol{w}}_2},{{\boldsymbol{Q}}_1},{{\boldsymbol{Q}}_2},\rho $ 已知$ {\boldsymbol{Q}}_1^{(i)},{\boldsymbol{Q}}_2^{(i)},{\rho ^{(i)}} $,求解问题P2,获得$ {\boldsymbol{w}}_1^{(i + 1)},{\boldsymbol{w}}_2^{(i + 1)} $ 已知$ {\boldsymbol{w}}_1^{(i + 1)},{\boldsymbol{w}}_2^{(i + 1)},{\boldsymbol{Q}}_2^{(i)},{\rho ^{(i)}} $,求解问题P4,获得$ {\boldsymbol{Q}}_1^{(i + 1)} $ 已知$ {\boldsymbol{w}}_1^{(i + 1)},{\boldsymbol{w}}_2^{(i + 1)},{\boldsymbol{Q}}_1^{(i + 1)},{\rho ^{(i)}} $,求解问题P6,获得
$ {\boldsymbol{Q}}_2^{(i + 1)} $已知$ {\boldsymbol{w}}_1^{(i + 1)},{\boldsymbol{w}}_2^{(i + 1)},{\boldsymbol{Q}}_1^{(i + 1)},{\boldsymbol{Q}}_2^{(i + 1)} $,求解问题P8,获得
$ {\rho ^{(i + 1)}} $更新$ i = i + 1 $ end for:收敛 -
[1] PRASAD R, MANTRI D S, PANDEY S K, et al. 6G Connectivity-Systems, Technologies, and Applications: Digitalization of New Technologies, 6G and Evolution[M]. Aalborg: River Publishers, 2024: 139–156. [2] SARKAR D, YOGITA, YADAV S S, et al. A comprehensive survey on IRS-assisted NOMA-based 6G wireless network: Design perspectives, challenges and future directions[J]. IEEE Transactions on Network and Service Management, 2024, 21(2): 2539–2562. doi: 10.1109/TNSM.2023.3348138. [3] AL-DWEIK A, ALSUSA E, DOBRE O A, et al. Multi-symbol rate NOMA for improving connectivity in 6G communications networks[J]. IEEE Communications Magazine, 2024, 62(7): 118–123. doi: 10.1109/MCOM.001.2300351. [4] DINH P, ARFAOUI M A, SHARAFEDDINE S, et al. A low-complexity framework for joint user pairing and power control for cooperative NOMA in 5G and beyond cellular networks[J]. IEEE Transactions on Communications, 2020, 68(11): 6737–6749. doi: 10.1109/TCOMM.2020.3009262. [5] BENBUK A A, KOUZAYHA N, COSTANTINE J, et al. Charging and wake-up of IoT devices using harvested RF energy with near-zero power consumption[J]. IEEE Internet of Things Magazine, 2023, 6(1): 162–167. doi: 10.1109/IOTM.001.2200202. [6] SHERAZI H H R, ZORBAS D, and O’FLYNN B. A comprehensive survey on RF energy harvesting: Applications and performance determinants[J]. Sensors, 2022, 22(8): 2990. doi: 10.3390/s22082990. [7] JAMEEL F, WYNE S, KADDOUM G, et al. A comprehensive survey on cooperative relaying and jamming strategies for physical layer security[J]. IEEE Communications Surveys & Tutorials, 2019, 21(3): 2734–2771. doi: 10.1109/COMST.2018.2865607. [8] 卢汉成, 王亚正, 赵丹, 等. 智能反射表面辅助的无线通信系统的物理层安全综述[J]. 通信学报, 2022, 43(2): 171–184. doi: 10.11959/j.issn.1000−436x.2022025.LU Hancheng, WANG Yazheng, ZHAO Dan, et al. Survey of physical layer security of intelligent reflecting surface-assisted wireless communication systems[J]. Journal on Communications, 2022, 43(2): 171–184. doi: 10.11959/j.issn.1000−436x.2022025. [9] FU Min, MEI Weidong, and ZHANG Rui. Multi-active/passive-IRS enabled wireless information and power transfer: Active IRS deployment and performance analysis[J]. IEEE Communications Letters, 2023, 27(8): 2217–2221. doi: 10.1109/LCOMM.2023.3287573. [10] CUI Miao, ZHANG Guangchi, and ZHANG Rui. Secure wireless communication via intelligent reflecting surface[J]. IEEE Wireless Communications Letters, 2019, 8(5): 1410–1414. doi: 10.1109/LWC.2019.2919685. [11] FANG Xingchen. Joint channel estimation algorithm for IRS-assisted multi-user MIMO systems[J]. IEEE Communications Letters, 2024, 28(2): 367–371. doi: 10.1109/LCOMM.2023.3346914. [12] DI RENZO M, ZAPPONE A, DEBBAH M, et al. Smart radio environments empowered by reconfigurable intelligent surfaces: How it works, state of research, and the road ahead[J]. IEEE Journal on Selected Areas in Communications, 2020, 38(11): 2450–2525. doi: 10.1109/JSAC.2020.3007211. [13] 季薇, 刘子卿. IRS辅助的异构SWIPT-NOMA系统资源分配方案[J]. 通信学报, 2024, 45(4): 39–53. doi: 10.11959/j.issn.1000-436x.2024027.JI Wei and LIU Ziqing. Resource allocation scheme for IRS assisted heterogeneous SWIPT-NOMA system[J]. Journal on Communications, 2024, 45(4): 39–53. doi: 10.11959/j.issn.1000-436x.2024027. [14] LI Zhendong, CHEN Wen, WU Qingqing, et al. Joint beamforming design and power splitting optimization in IRS-assisted SWIPT NOMA networks[J]. IEEE Transactions on Wireless Communications, 2022, 21(3): 2019–2033. doi: 10.1109/TWC.2021.3108901. [15] GOKTAS M B, DURSUN Y, and DING Zhiguo. IRS and SWIPT-assisted full-duplex NOMA for 6G umMTC[J]. IEEE Transactions on Green Communications and Networking, 2023, 7(4): 1957–1970. doi: 10.1109/TGCN.2023.3289505. [16] LIU Qiuyan, LU Manchun, LI Na, et al. Joint beamforming and power splitting optimization for RIS-assited cooperative SWIPT NOMA systems[C]. 2022 IEEE Wireless Communications and Networking Conference, Austin, USA, 2022: 351–356. doi: 10.1109/WCNC51071.2022.9771850. [17] SAMY M, AI-HRAISHAWI H, KISSELEFF S, et al. Multiple RIS-assisted cooperative NOMA with user selection[C]. 2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 2023: 1405–1410. doi: 10.1109/GLOBECOM54140.2023.10437225. [18] 朱政宇, 徐金雷, 孙钢灿, 等. 基于IRS辅助的SWIPT物联网系统安全波束成形设计[J]. 通信学报, 2021, 42(4): 185–193. doi: 10.11959/j.issn.1000-436x.2021060.ZHU Zhengyu, XU Jinlei, SUN Gangcan, et al. Secure beamforming design for IRS-assisted SWIPT Internet of Things system[J]. Journal on Communications, 2021, 42(4): 185–193. doi: 10.11959/j.issn.1000-436x.2021060. [19] SHEN Yanyan, WANG Chunjie, ZANG Weilin, et al. Outage constrained max-min secrecy rate optimization for IRS-aided SWIPT systems with artificial noise[J]. IEEE Internet of Things Journal, 2024, 11(6): 9814–9828. doi: 10.1109/JIOT.2023.3325362. [20] HAN Hui, CAO Yang, SHENG Min, et al. IRS-aided secure MISO-NOMA networks towards internal and external eavesdropping[C]. 2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 2022: 4364–4370. doi: 10.1109/GLOBECOM48099.2022.10000742. [21] XIAO Liang, HONG Siyuan, XU Shiyu, et al. IRS-aided energy-efficient secure WBAN transmission based on deep reinforcement learning[J]. IEEE Transactions on Communications, 2022, 70(6): 4162–4174. doi: 10.1109/TCOMM.2022.3169813. [22] LI Baogang, SI Fuqiang, HAN Dongsheng, et al. IRS-aided SWIPT systems with power splitting and artificial noise[J]. China Communications, 2022, 19(4): 108–120. doi: 10.23919/JCC.2022.04.009. [23] PERERA T D P, JAYAKODY D N K, SHARMA S K, et al. Simultaneous wireless information and power transfer (SWIPT): Recent advances and future challenges[J]. IEEE Communications Surveys & Tutorials, 2018, 20(1): 264–302. doi: 10.1109/COMST.2017.2783901. [24] TANG Jie, LUO Jingci, LIU Mingqian, et al. Energy efficiency optimization for NOMA with SWIPT[J]. IEEE Journal of Selected Topics in Signal Processing, 2019, 13(3): 452–466. doi: 10.1109/JSTSP.2019.2898114. [25] LI Qiang, HONG Mingyi, WAI H T, et al. Transmit solutions for MIMO wiretap channels using alternating optimization[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(9): 1714–1727. doi: 10.1109/JSAC.2013.130906. [26] REN Juanjuan, LEI Xianfu, PENG Zhangjie, et al. RIS-assisted cooperative NOMA with SWIPT[J]. IEEE Wireless Communications Letters, 2023, 12(3): 446–450. doi: 10.1109/LWC.2022.3229843. [27] XU Yanqing, SHEN Chao, DING Zhiguo, et al. Joint beamforming and power-splitting control in downlink cooperative SWIPT NOMA systems[J]. IEEE Transactions on Signal Processing, 2017, 65(18): 4874–4886. doi: 10.1109/TSP.2017.2715008. [28] WU Qingqing and ZHANG Rui. Joint active and passive beamforming optimization for intelligent reflecting surface assisted SWIPT Under QoS Constraints[J]. IEEE Journal on Selected Areas in Communications, 2020, 38(8): 1735–1748. doi: 10.1109/JSAC.2020.3000807. [29] CAO Pan, THOMPSON J, and POOR H V. A sequential constraint relaxation algorithm for rank-one constrained problems[C]. The 25th European Signal Processing Conference, Kos, Greece, 2017: 1060–1064. doi: 10.23919/EUSIPCO.2017.8081370. [30] BEN-TAL A and NEMIROVSKIAEI A S. Lectures on Modern Convex Optimization: Analysis, Algorithms, and Engineering Applications[M]. Philadelphia, USA: Society for Industrial and Applied Mathematics, 2001. [31] BOYD S and VANDENBERGHE L. Convex Optimization[M]. Cambridge: Cambridge University Press, 2004. -





 下载:
下载:





 下载:
下载:
