Adaptive Clustering Center Selection: A Privacy Utility Balancing Method for Federated Learning
-
摘要: 联邦学习是一种分布式机器学习方法,它使多个设备或节点能够协作训练模型,同时保持数据的本地性。但由于联邦学习是由不同方拥有的数据集进行模型训练,敏感数据可能会被泄露。为了改善上述问题,已有相关工作在联邦学习中应用差分隐私对梯度数据添加噪声。然而在采用了相应的隐私技术来降低敏感数据泄露风险的同时,模型精度和效果因为噪声大小的不同也受到了部分影响。为解决此问题,该文提出一种自适应聚类中心个数选择机制(DP-Fed-Adap),根据训练轮次和梯度的变化动态地改变聚类中心个数,使模型可以在保持相同性能水平的同时确保对敏感数据的保护。实验表明,在使用相同的隐私预算前提下DP-Fed-Adap与添加了差分隐私的联邦相似算法(FedSim)和联邦平均算法(FedAvg)相比,具有更好的模型性能和隐私保护效果。Abstract:
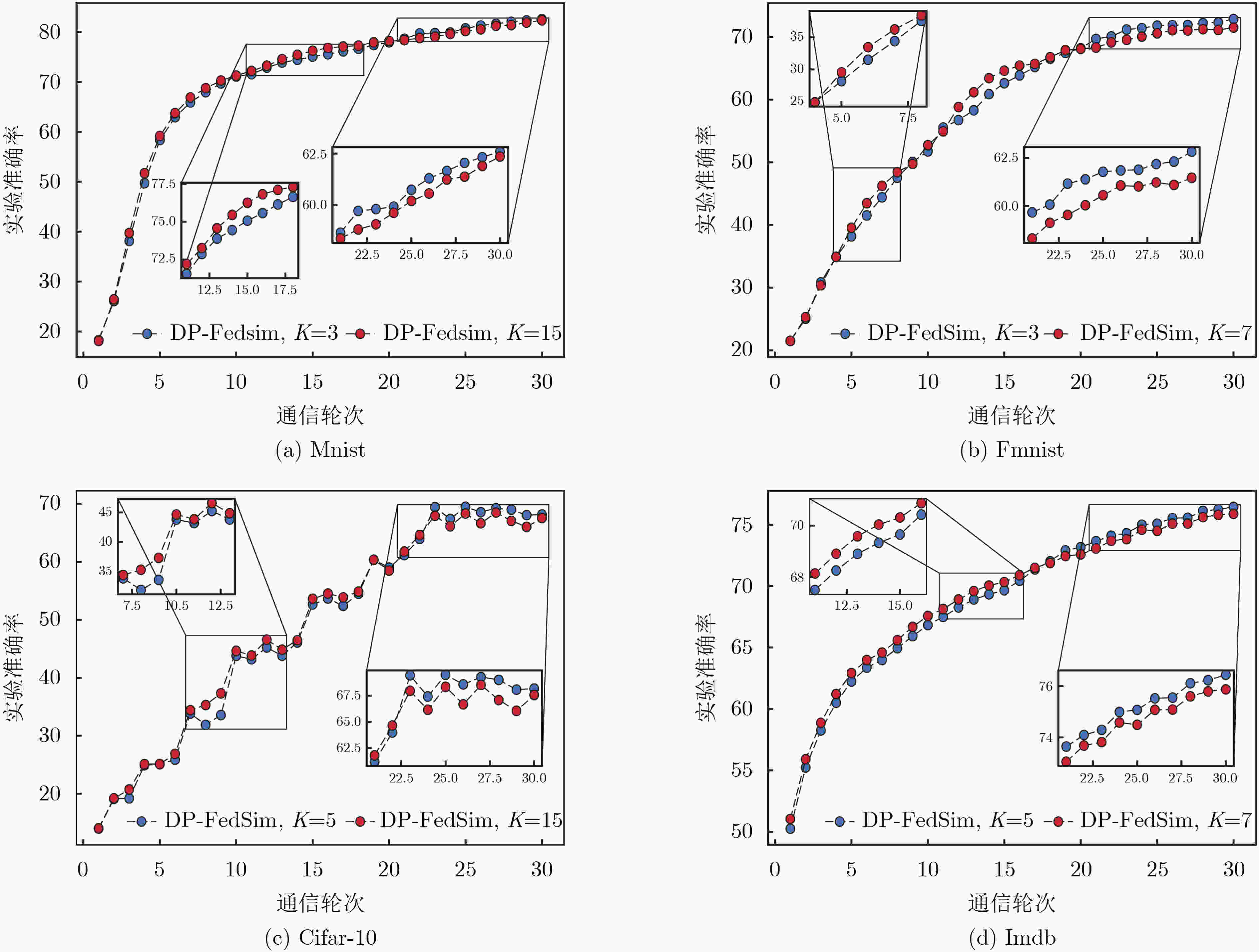
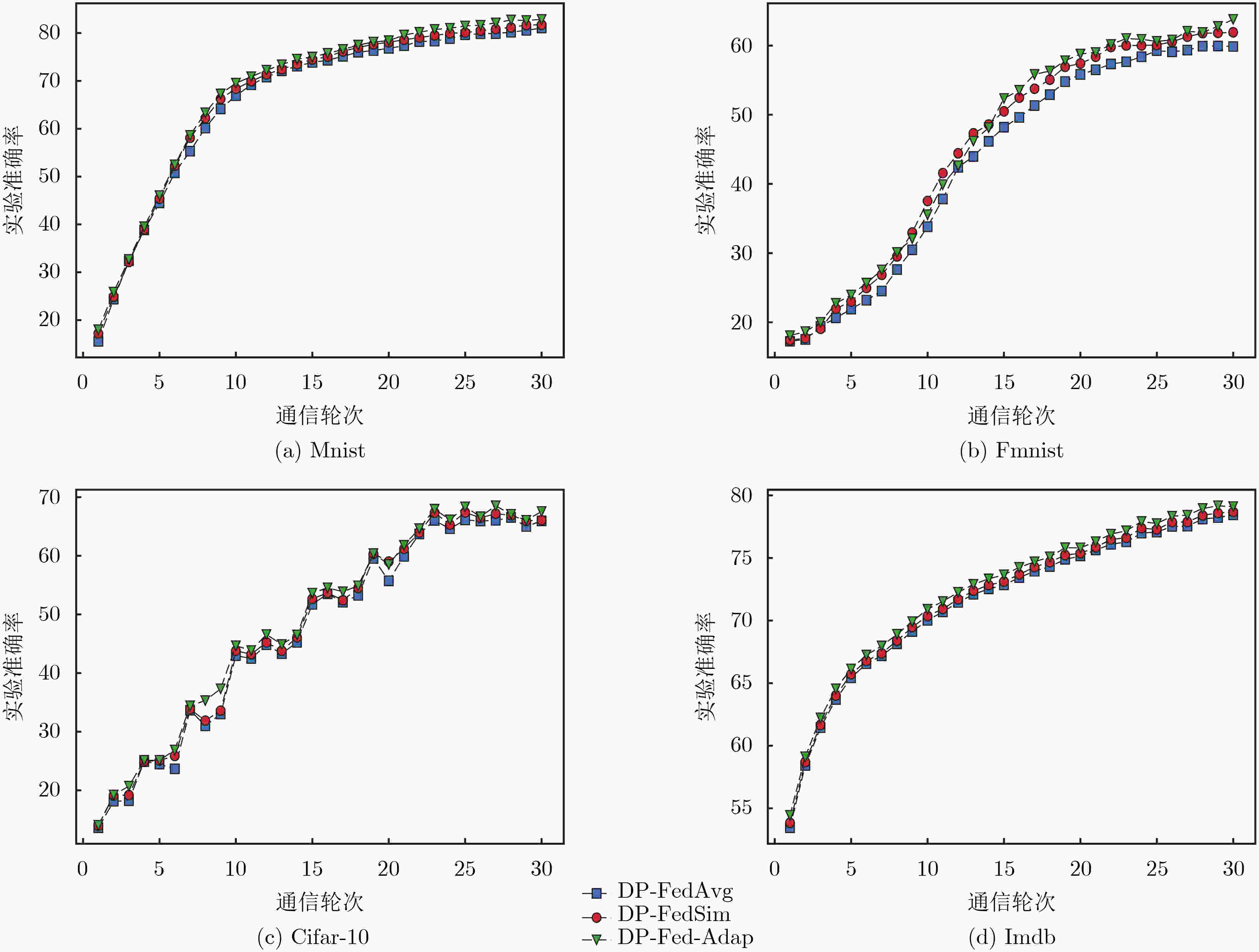
Objective Differential privacy, based on strict statistical models, is widely applied in federated learning. The common approach integrates privacy protection by perturbing parameters during local model training and global model aggregation to safeguard user privacy while maintaining model performance. A key challenge is minimizing performance degradation while ensuring strong privacy protection. Currently, an issue arises in early-stage training, where data gradient directions are highly dispersed. Directly applying initial data calculations and processing at this stage can reduce the accuracy of the global model. Methods To address this issue, this study introduces a differential privacy mechanism in federated learning to protect individual privacy while clustering gradient information from multiple data owners. During gradient clustering, the number of clustering centers is dynamically adjusted based on training epochs, with the rate of change in clusters aligned with the model training process. In the early stages, higher noise levels are introduced to enhance privacy protection. As the model converges, noise is gradually reduced to improve learning of the true data distribution. Result and discussions The first set of experimental results ( Fig. 3 ) shows that different fixed numbers of cluster centers lead to varying rates of change in training accuracy during the early and late stages of the training cycle. This suggests that reducing the number of cluster centers as training progresses benefits model performance, and the segmentation function is selected based on these findings. The second set of experiments (Fig. 4 ) indicates that among four sets of model performance comparisons, our method achieves the highest accuracy in the later stages of training as the number of rounds increases. This demonstrates that adjusting the number of cluster centers during training has a measurable effect. As model training concludes, gradient directions tend to converge, and reducing the number of cluster centers improves accuracy. The performance comparison of the three models (Table 2 ) further shows that our proposed method outperforms others in most cases.Conclusions Comparative experiments on four publicly available datasets demonstrate that the proposed algorithm outperforms baseline methods in model performance after incorporating adaptive clustering center selection. Additionally, it ensures privacy protection for sensitive data while maintaining a more stable training process. The improved clustering strategy better aligns with the actual training dynamics, validating the effectiveness of this approach. -
1 DP-Fed-Adap算法
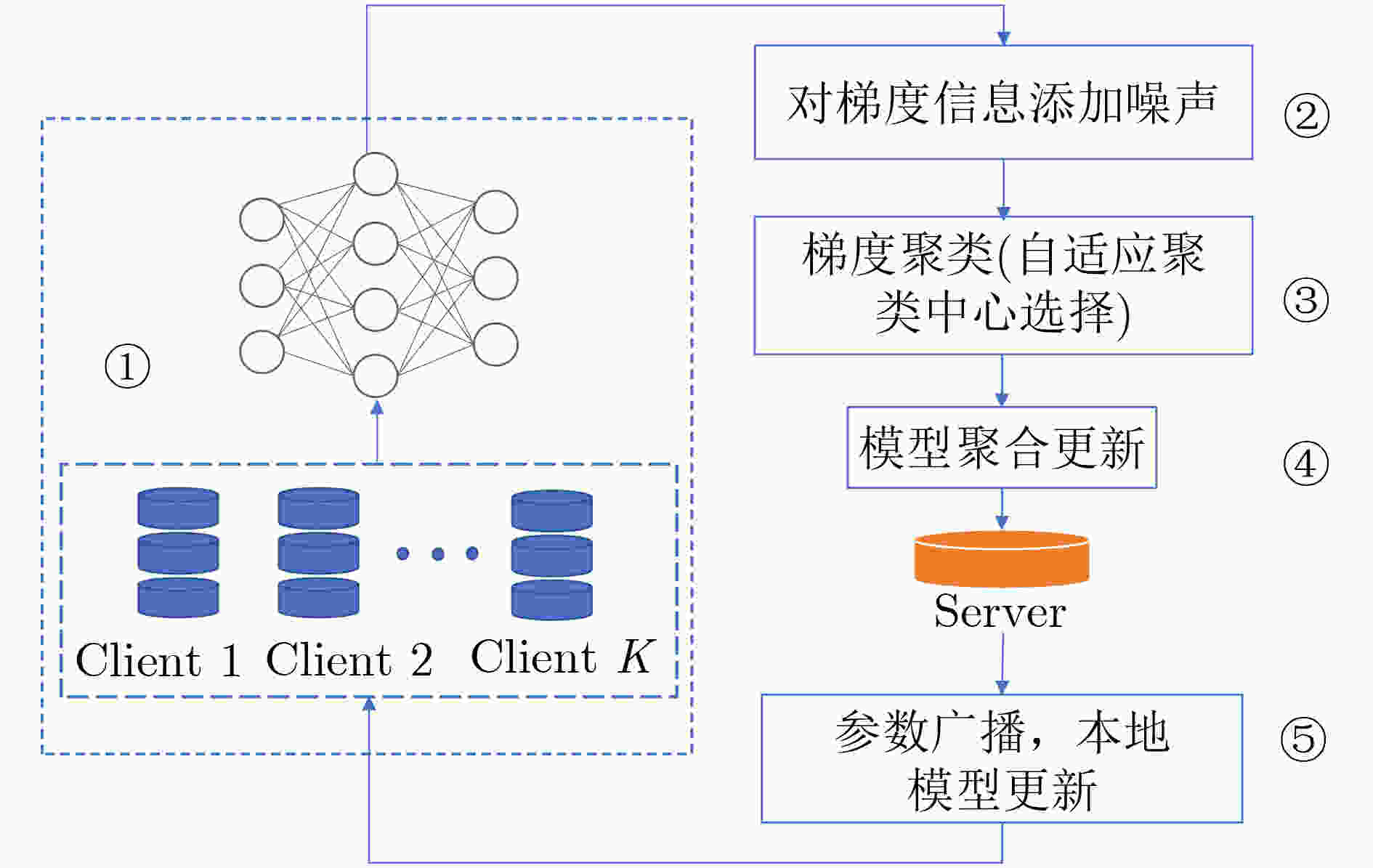
输入:训练样本:$ \{ ({x_1},{y_1}),({x_2},{y_2}), \cdots ,({x_i},{y_i})\} $ 学习率:$ a $;模型初始参数:$ {{\boldsymbol{\theta}} _{\text{0}}} $ 本地更新迭代数:$ T $;梯度裁剪值:$ {{C}} $ 初始聚类中心个数:$ K $;服务器个数:$ N $ 输出:迭代后的模型参数:$ {{\boldsymbol{\theta}} _T} $ (1) 随机选择几个客户端参与模型训练 (2) 每个客户端随机初始化模型参数$ {{\boldsymbol{\theta}} _{\text{0}}} $ (3) for对每一轮的迭代t=1, 2,···, $ T $,执行如下操作do (4) 采集一个样本大小为$ m $的集合$ B $: (5) for对每一个样本$ ({x_i},{y_i}) \in B $: (6) 求梯度值:$ {{\boldsymbol{g}}_i} \leftarrow \nabla L(F({x_i},{{\boldsymbol{\theta}} _i}),{y_i}) $ (7) 梯度裁剪:$ {{\boldsymbol{g}}'_i} \leftarrow {{\boldsymbol{g}}_i}/\max (1,{{{{\left\| {{{\boldsymbol{g}}_i}} \right\|}_2}} \mathord{\left/ {\vphantom {{{{\left\| {{g_i}} \right\|}_2}} {\text{C}}}} \right. } {{C}}}) $ (8) end (9) 敏感值计算:$ \Delta {f}=2\times {C} $ (10) 梯度添加噪声:$ {{\boldsymbol{g}}'_i} \leftarrow {{\boldsymbol{g}}_i} + {\boldsymbol{N}}(0,\sigma _t^2{{{C}}^2}{\boldsymbol{I}}) $ (11) for 对所得到的加噪后的梯度信息: (12) 自适应聚类中心个数选择方法 (13) 各个服务器梯度信息做聚合操作:
$ {g'_i} = 1/N \displaystyle\sum\nolimits_{n = 1}^N {{{g}'_{in}}} $(14) 更新模型参数:$ {\theta _{{{t}} + {\text{1}}}} = {\theta _{{t}}} - {\text{a}}{g'_i} $ (15) end (16)end 2 Adaptive algorithm算法
输入:样本集:$ \{ {{\boldsymbol{g}}_1},{{\boldsymbol{g}}_2}, \cdots ,{{\boldsymbol{g}}_m}\} $;初始聚类中心个数:$ {{K}} $ 本地更新迭代数:$ {T} $ 输出:簇划分:$ \{ {{\boldsymbol{B}}_1},{{\boldsymbol{B}}_2}, \cdots ,{{\boldsymbol{B}}_{{K}}}\} $ (1)for对每一轮的迭代t=1, 2,···, $ T $,执行如下操作do (2) for从数据集中选择$ K $个样本作为初始聚类中心
$ \{{\boldsymbol{g}}_{1},{\boldsymbol{g}}_{2},\cdots, {\boldsymbol{g}}_{{K}}\} $(3) $ {B_i} = \varnothing (1 \le i \le K) $ (4) for j=1, 2,···, m do (5) 计算$ {{\boldsymbol{g}}_j} $与各个聚类中心$ {B_j} $的距离:$ d = {\left\| {{{\boldsymbol{g}}_j} - {{\boldsymbol{B}}_j}} \right\|_2} $ (6) 根据距离最近的均值向量确定$ {{\boldsymbol{g}}_j} $属于哪一个簇 (7) 将$ {{\boldsymbol{g}}_j} $划入相应的簇中 (8) end (9) for i=1, 2,···, $ K $ do (10) 计算新的均值向量:$ {{\boldsymbol{g}}'_i} = \dfrac{1}{{\left\|{{\boldsymbol{B}}_i}\right\|}}\displaystyle\sum {\boldsymbol{g}} $ (11) if $ {{\boldsymbol{g}}'_i} \ne {{\boldsymbol{g}}_i} $ then (12) 将均值向量更新 (13) else (14) 保持均值向量不变 (15) end (16) $ K = K - \left[\dfrac{{{\text{iter}}}}{K}\right] $ (17) until均值向量均未更新 (18) end (19) end 表 1 聚类中心个数随轮次变化情况
1~5轮 5~10轮 10~20轮 20~30轮 Mnist 5 4 3 2 Fmnist 7 6 5 4 Cifar-10 5 4 3 2 Imdb 5 4 3 2 表 2 3种模型性能对比(%)
数据集 模型 $\varepsilon $ =2.53, Accuracy $\varepsilon $=3.58, Accuracy DP-FedAvg DP-FedSim DP-Fed-Adap DP-FedAvg DP-FedSim DP-Fed-Adap Mnist
MnistMLP 81.04 81.72 82.83 84.59 85.35 85.59 CNN 89.76 90.46 92.84 91.37 92.04 93.87 Fmnist
FmnistMLP 59.86 61.90 63.77 62.63 64.34 65.76 CNN 92.89 91.60 92.04 93.36 94.57 93.06 Cifar-10 CNN 65.95 66.08 67.56 67.54 68.51 68.45 Imdb LSTM 78.44 78.67 79.10 81.29 81.44 81.74 -
[1] 李三希, 曹志刚, 崔志伟, 等. 数字经济的博弈论基础性科学问题[J]. 中国科学基金, 2021, 35(5): 782–800. doi: 10.16262/j.cnki.1000-8217.2021.05.021.LI Sanxi, CAO Zhigang, CUI Zhiwei, et al. Fundamental scientific problems of game theory for the digital economy[J]. Bulletin of National Natural Science Foundation of China, 2021, 35(5): 782–800. doi: 10.16262/j.cnki.1000-8217.2021.05.021. [2] 刘艺璇, 陈红, 刘宇涵, 等. 联邦学习中的隐私保护技术[J]. 软件学报, 2022, 33(3): 1057–1092. doi: 10.13328/j.cnki.jos.006446.LIU Yixuan, CHEN Hong, LIU Yuhan, et al. Privacy-preserving techniques in federated learning[J]. Journal of Software, 2022, 33(3): 1057–1092. doi: 10.13328/j.cnki.jos.006446. [3] TRAN A T, LUONG T D, KARNJANA J, et al. An efficient approach for privacy preserving decentralized deep learning models based on secure multi-party computation[J]. Neurocomputing, 2021, 422: 245–262. doi: 10.1016/j.neucom.2020.10.014. [4] WANG Bolun, YAO Yuanshun, SHAN S, et al. Neural cleanse: Identifying and mitigating backdoor attacks in neural networks[C]. 2019 IEEE Symposium on Security and Privacy, San Francisco, USA, 2019: 707–723. doi: 10.1109/SP.2019.00031. [5] YAN Zhigang and LI Dong. Performance analysis for resource constrained decentralized federated learning over wireless networks[J]. IEEE Transactions on Communications, 2024, 72(7): 4084–4100. doi: 10.1109/TCOMM.2024.3362143. [6] YAN Zhigang, LI Dong, ZHANG Zhichao, et al. Accuracy–security tradeoff with balanced aggregation and artificial noise for wireless federated learning[J]. IEEE Internet of Things Journal, 2023, 10(20): 18154–18167. doi: 10.1109/JIOT.2023.3277632. [7] YAN Zhigang and LI Dong. Decentralized federated learning on the edge: From the perspective of quantization and graphical topology[J]. IEEE Internet of Things Journal, 2024, 11(21): 34172–34186. doi: 10.1109/JIOT.2024.3400512. [8] WU Nan, FAROKHI F, SMITH D, et al. The value of collaboration in convex machine learning with differential privacy[C]. 2020 IEEE Symposium on Security and Privacy, San Francisco, USA, 2020: 304–317. doi: 10.1109/SP40000.2020.00025. [9] DWORK C. Differential privacy[C]. The 33rd International Colloquium on Automata, Languages and Programming, Venice, Italy, 2006: 1–12. doi: 10.1007/11787006_1. [10] 张跃, 朱友文, 周玉倩, 等. (ε, δ)-本地差分隐私模型下的均值估计机制[J]. 电子与信息学报, 2023, 45(3): 765–774. doi: 10.11999/JEIT221047.ZHANG Yue, ZHU Youwen, ZHOU Yuqian, et al. Mean estimation mechanisms under (ε, δ)-local differential privacy[J]. Journal of Electronics and Information Science, 2023, 45(3): 765–774. doi: 10.11999/JEIT221047. [11] ABADI M, CHU A, GOODFELLOW I J, et al. Deep learning with differential privacy[C]. 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 2016: 308–318. doi: 10.1145/2976749.2978318. [12] 郭鹏, 钟尚平, 陈开志, 等. 差分隐私GAN梯度裁剪阈值的自适应选取方法[J]. 网络与信息安全学报, 2018, 4(5): 10–20. doi: 10.11959/j.issn.2096-109x.2018041.GUO Peng, ZHONG Shangping, CHEN Kaizhi, et al. Adaptive selection method of differential privacy GAN gradient clipping thresholds[J]. Journal of Network and Information Security, 2018, 4(5): 10–20. doi: 10.11959/j.issn.2096-109x.2018041. [13] YANG Xiaodong, ZHANG Huishuai, CHEN Wei, et al. Normalized/clipped SGD with perturbation for differentially private non-convex optimization[EB/OL]. https://arxiv.org/abs/2206.13033. [14] WU Shuhui, YU Mengqing, AHMED M A M, et al. FL-MAC-RDP: Federated learning over multiple access channels with Rényi differential privacy[J]. International Journal of Theoretical Physics, 2021, 60(7): 2668–2682. doi: 10.1007/s10773-021-04867-0. [15] MIRONOV I. Rényi differential privacy[C]. 2017 IEEE 30th Computer Security Foundations Symposium, Santa Barbara, USA, 2017: 263–275. doi: 10.1109/CSF.2017.11. [16] HAN Andi, MISHRA B, JAWANPURIA P, et al. Differentially private Riemannian optimization[J]. Machine Learning, 2024, 113(3): 1133–1161. doi: 10.1007/s10994-023-06508-5. [17] LI Tian, SAHU A K, ZAHEER M, et al. Federated optimization in heterogeneous networks[J]. Proceedings of Machine Learning and Systems, 2020, 2: 429–450. [18] LI Xiaoxiao, JIANG Meirui, ZHANG Xiaofei, et al. FedBN: Federated learning on non-IID features via local batch normalization[C]. The 9th International Conference on Learning Representations, Vienna, Austria, 2021: 1–27. [19] LEOUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278–2324. doi: 10.1109/5.726791. [20] HAN Xiao, RASUL K, VOLLGRAF R. Fashion-MNIST: A novel image dataset for benchmarking machine learning algorithms[EB/OL]. https://arxiv.org/abs/1708.07747. [21] KRIZHEVSKY A, HINTON G. Learning multiple layers of features from tiny images[J]. Handbook of Systemic Autoimmune Diseases, 2009, 1(4). [22] MCMAHAN B, MOORE E, RAMAGE D, et al. Communication-efficient learning of deep networks from decentralized data[C]. The 20th International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, USA, 2017: 1273–1282. [23] PALIHAWADANA C, WIRATUNGA N, WIJEKOON A, et al. FedSim: Similarity guided model aggregation for Federated Learning[J]. Neurocomputing, 2022, 483: 432–445. doi: 10.1016/j.neucom.2021.08.141. -





 下载:
下载:


 下载:
下载:
